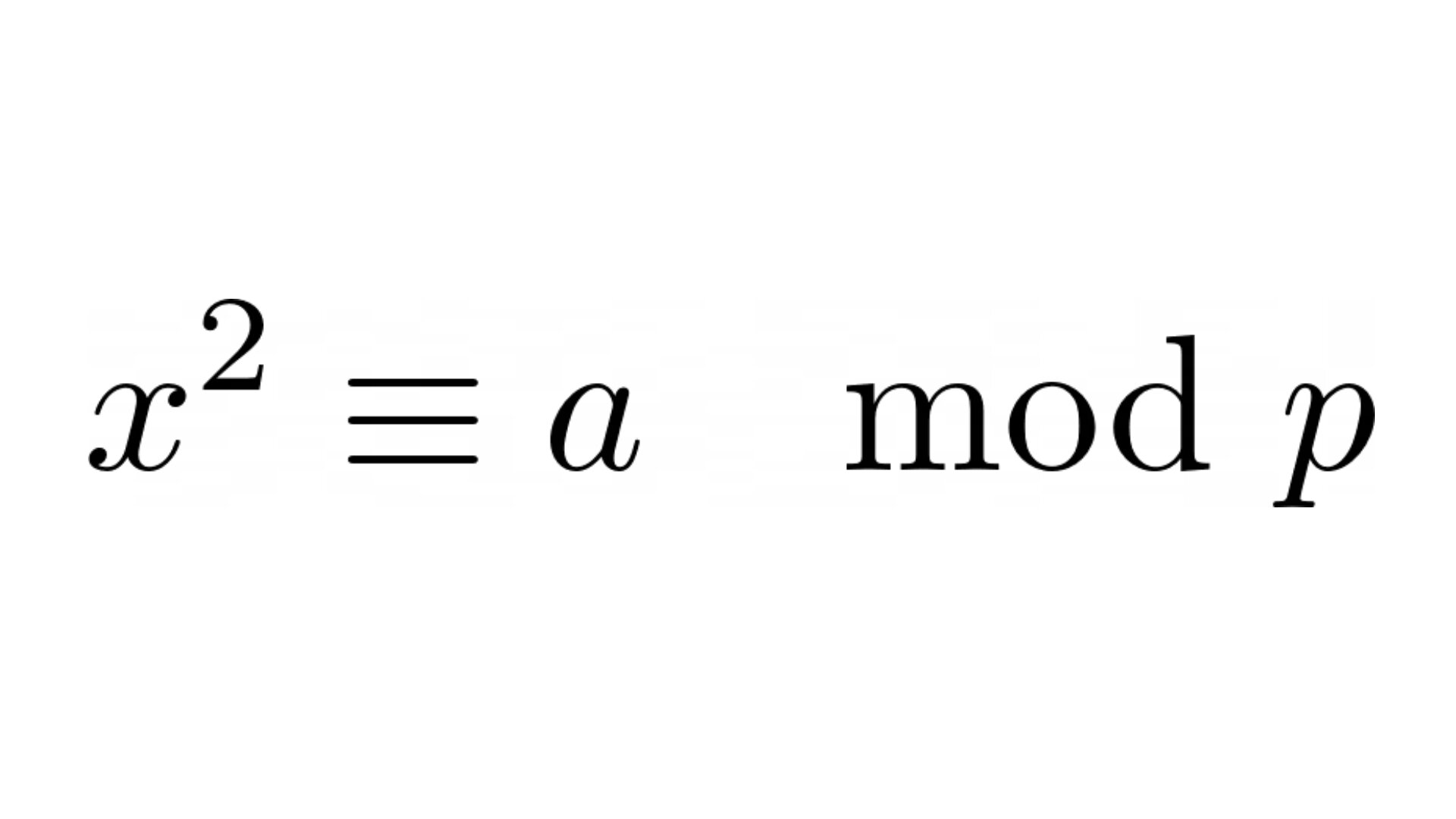This post is about the problem of computing square roots modulo a prime number, a well-known problem in algebra and number theory. Nowadays multiple highly-efficient algorithms have been developed to solve this problem, e.g. Tonelli-Shanks, Cipolla’s algorithms. In this post we will focus on one of the most prominent algorithms, namely the Tonelli-Shanks algorithm, which is often described in a rather complicated way in the literature, although its derivation and the idea behind it is actually simple and elegant. The goal of this post is to showcase this beauty of the theory and to then show how the Tonelli-Shanks algorithm can be implemented in Python. We also discuss some interesting connections of this problem to cryptography.
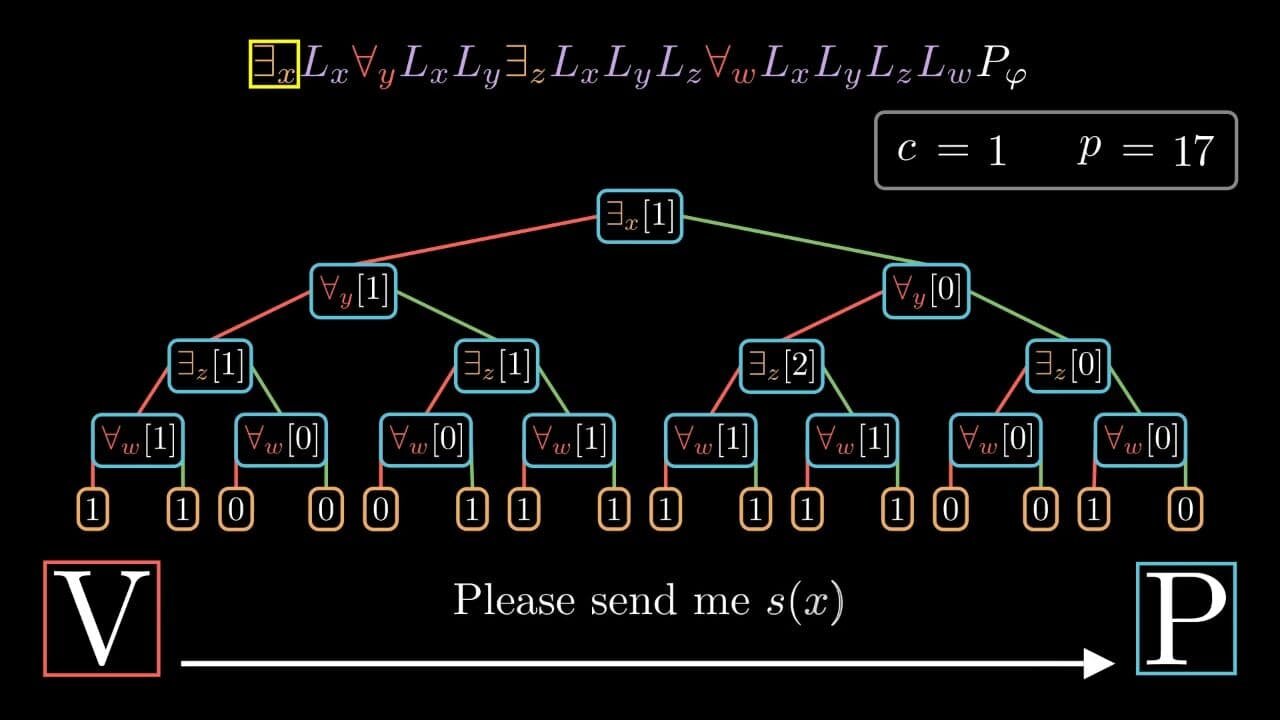
In complexity theory, it is well known that IP = PSPACE. In this post I would like to go over the private coin interactive protocol for TQBF typically used to prove that PSPACE is contained in IP and, in that context, present my detailed visualization of the entire protocol together with the Open Source tool I developed to run the protocol and render the animations. I would also like to note that when I was first studying the proof protocol for TQBF, I was a bit frustrated by the fact that most texts lack a precise and detailed description of some subtleties in the proof — this is what also motivated me to try my best to fill in the relevant but missing details in this post.
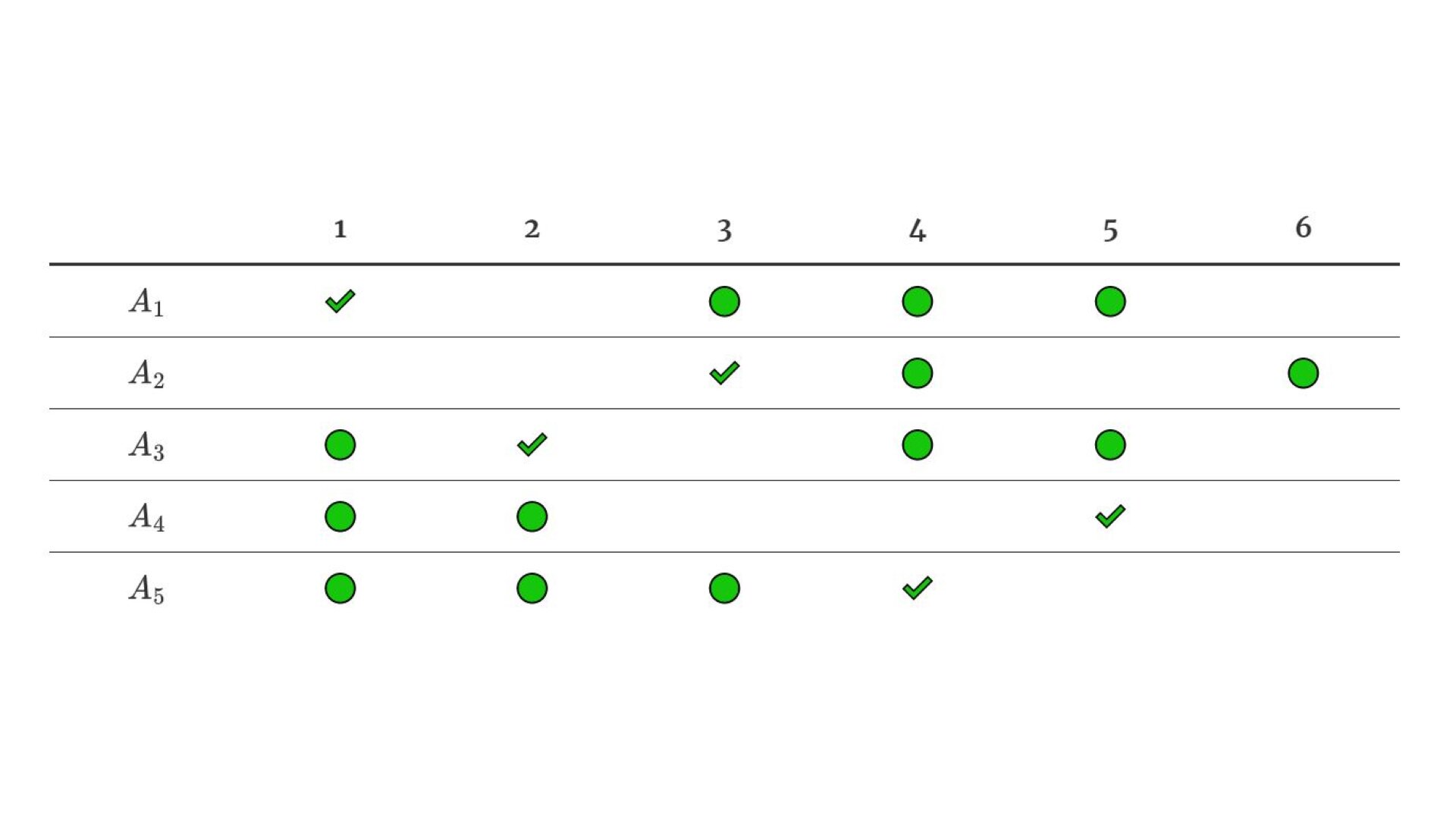
This post is about an interesting problem I recently tried to solve efficiently but ended up proving its NP-completeness. Informally, the problem is to find an injective mapping between two finite sets with certain, statically defined properties for values. For example, if A={a,b,c,d} and B={1,2,3,4,5}, we may want to find an injective mapping f:A→B with restrictions f(a)∈{1,3,4,5}, f(b)∈{3,4,5}, f(c)∈{1,2,4,5}, f(d)∈{1,2,5}, f(e)∈{1,2,3,4}. I find this problem of particular interest, because its nature is in my opinion very different compared to well-known NP-complete problems proven to be so by Karp. In this post we will visualize and formalize this problem, prove its NP-completeness and, finally, derive some interesting corollaries.
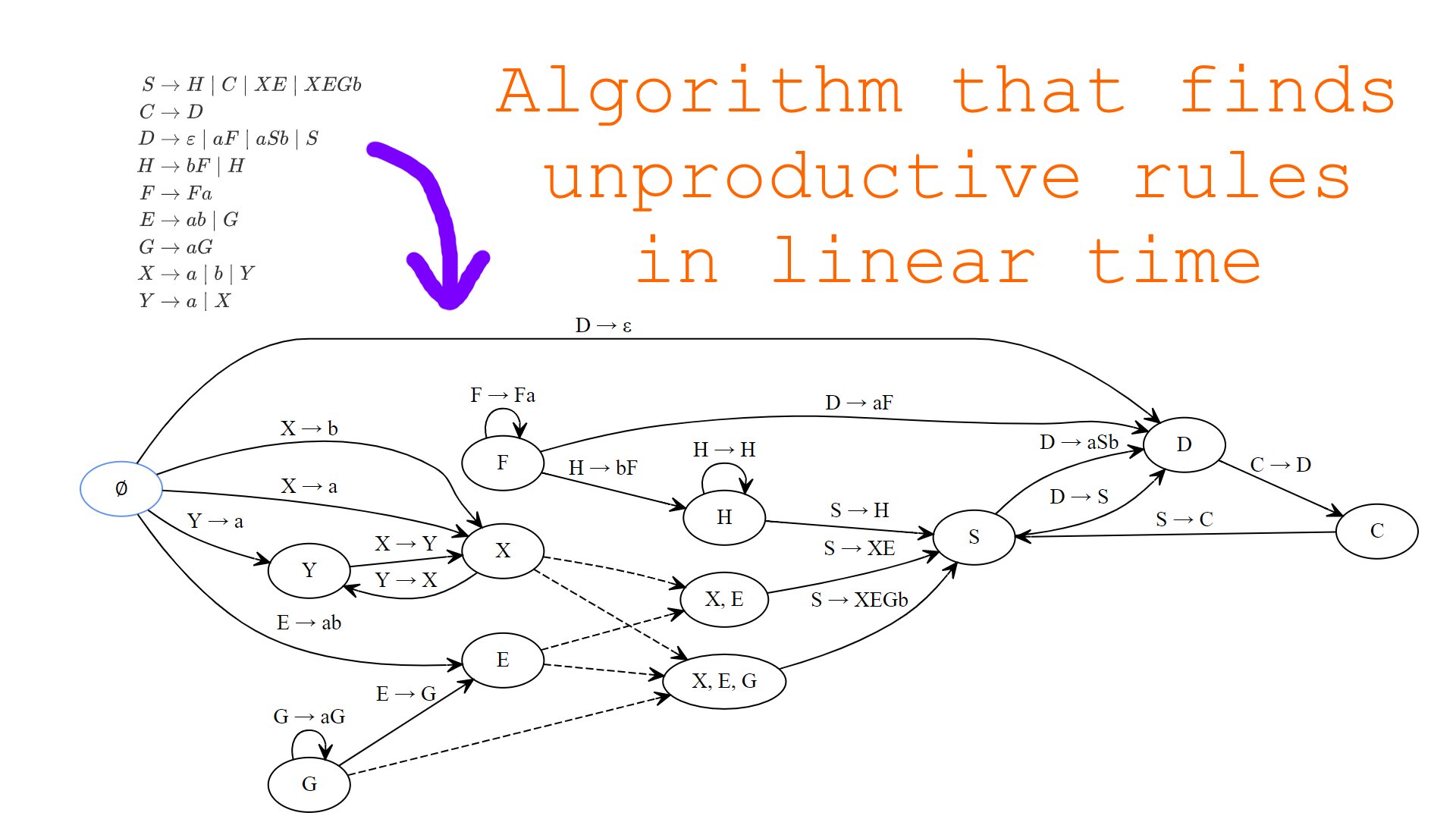
In programs that somehow deal with context-free grammars automatically, we may want to check whether some part of the grammar “makes sense” and isn’t totally redundant and useless. In other words, we may want to check whether some non-terminal or production can come up in some arbitrary sentential form. This problem arises often when the program we are implementing accepts user-defined grammars. In this post, we will consider an existing algorithm that solves the problem as well as introduce and implement a new, more efficient algorithm that detects useless parts of an input grammar.
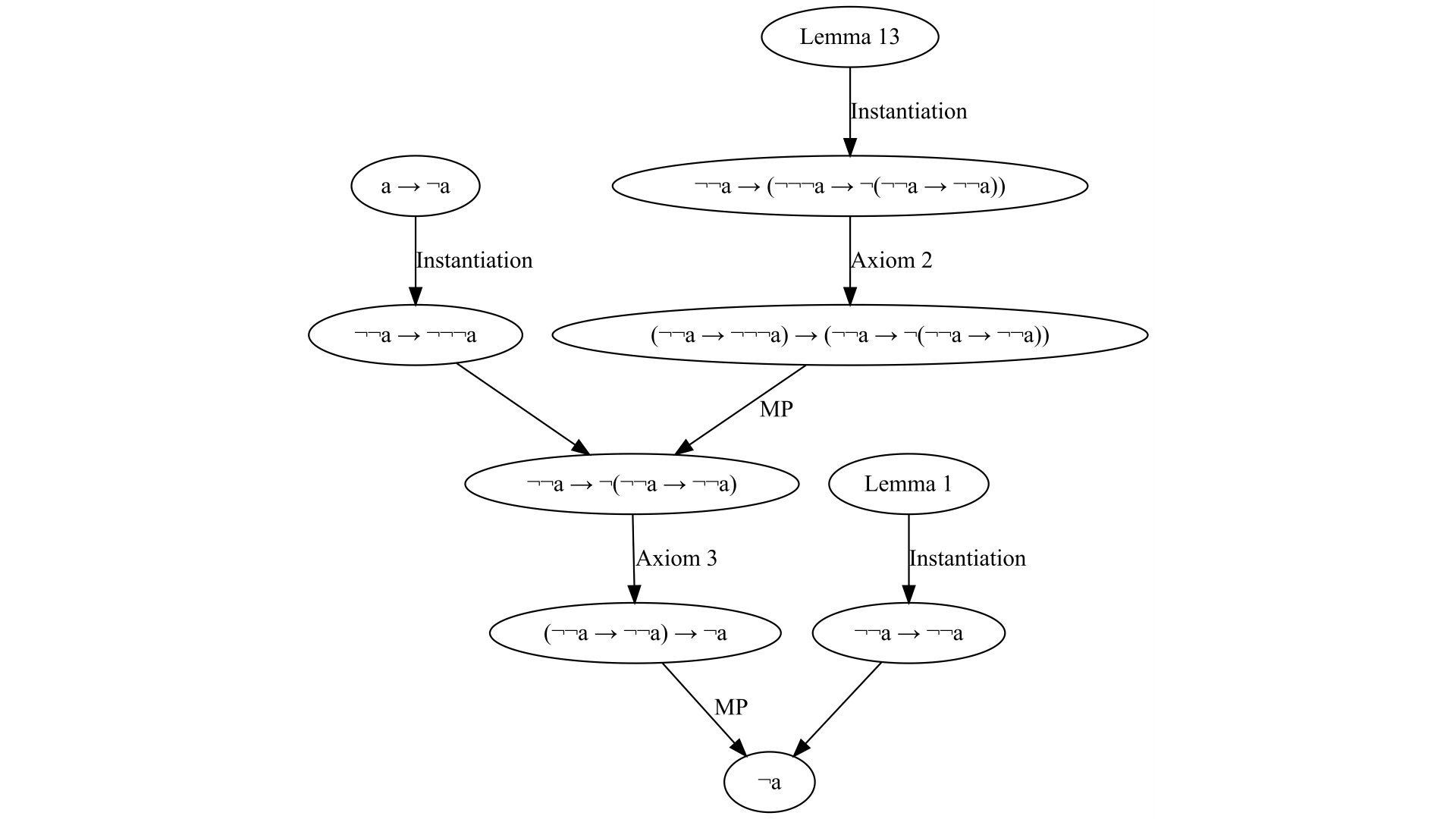
There exist different kinds of deductive systems in logic. Every deductive system consists of certain axioms and rules of inference. The problem of constructing a proof in every such system is quite difficult — computationally it is NP-Hard, since satisfiability can be reduced to it. So it is a good idea to trade-off between logical axioms and inference rules. Hilbert (Frege)-style proof systems are interesting because most of them use several axioms but only one inference rule — modus ponens, unlike, for example, Gentzen natural deduction. In other words, Hilbert-style proof systems “push” all the complexity of constructing a proof into the axioms — it is hard to syntactically instantiate them, but once done it is easier to combine them as there is only one rule of inference — modus ponens. In this post, I will present a notation for these Hilbert-style proofs I came up with recently, that allows one to construct them in a more systematic way, with less “guessing”.
The SAT problem is the first problem proven to be NP-Complete. However, many instances of this problem with certain properties can be solved efficiently in polynomial time. Well-known examples of such easy instances are 2-sat and horn formulas. All clauses in a 2-sat formula have at most 2 literals and horn-formulas consist only of clauses that contain at most one positive literal. In other words, a 2-sat clause is a conjunction of two implications and any horn clause can be rewritten as a conjunction of positive literals that implies either false or a negative literal. It may seem that satisfiability of formulas containing both 2-sat as well as horn clauses can be decided in polynomial time, however, because of the NP-completeness that we will prove shortly, this is not the case unless P=NP. The problem also remains NP-complete for Dual-horn clauses instead of normal horn clauses.
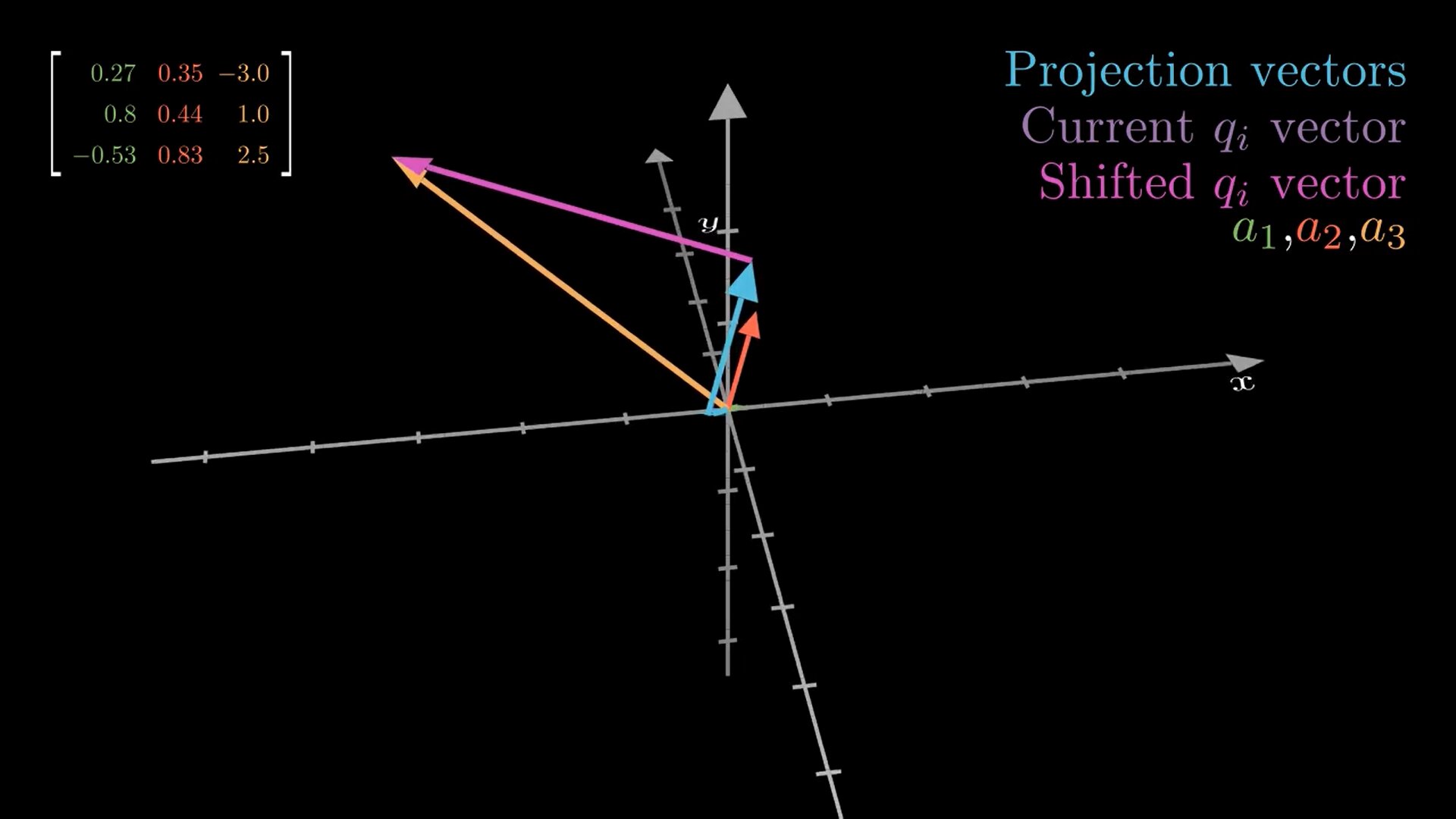
In linear algebra, orthogonal bases have many beautiful properties. For example, matrices consisting of orthogonal column vectors (a. k. a. orthogonal matrices) can be easily inverted by just transposing the matrix. Also, it is easier for example to project vectors on subspaces spanned by vectors that are orthogonal to each other. The Gram-Schmidt process is an important algorithm that allows us to convert an arbitrary basis to an orthogonal one spanning the same subspace. In this post, we will implement and visualize this algorithm in 3D with a popular Open-Source library manim.
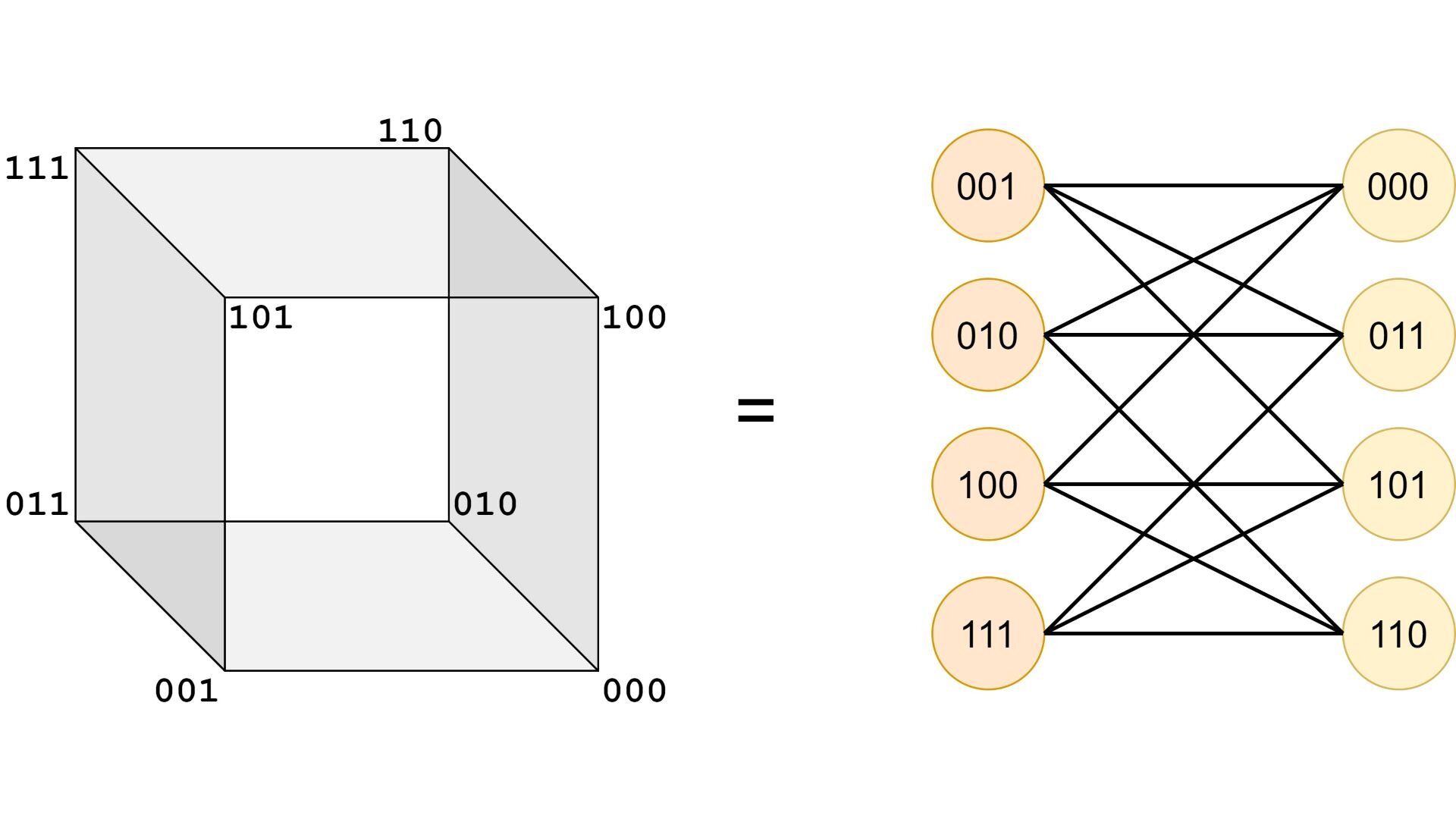
In this post I will introduce an interesting connection between gray codes and the problem of minimizing propositional logic formulas in disjunctive normal forms (DNF’s). Both of these concepts are related to the Hamming distance between two binary sequences, which is the amount of bits that need to be flipped in one sequence in order to obtain the other one.
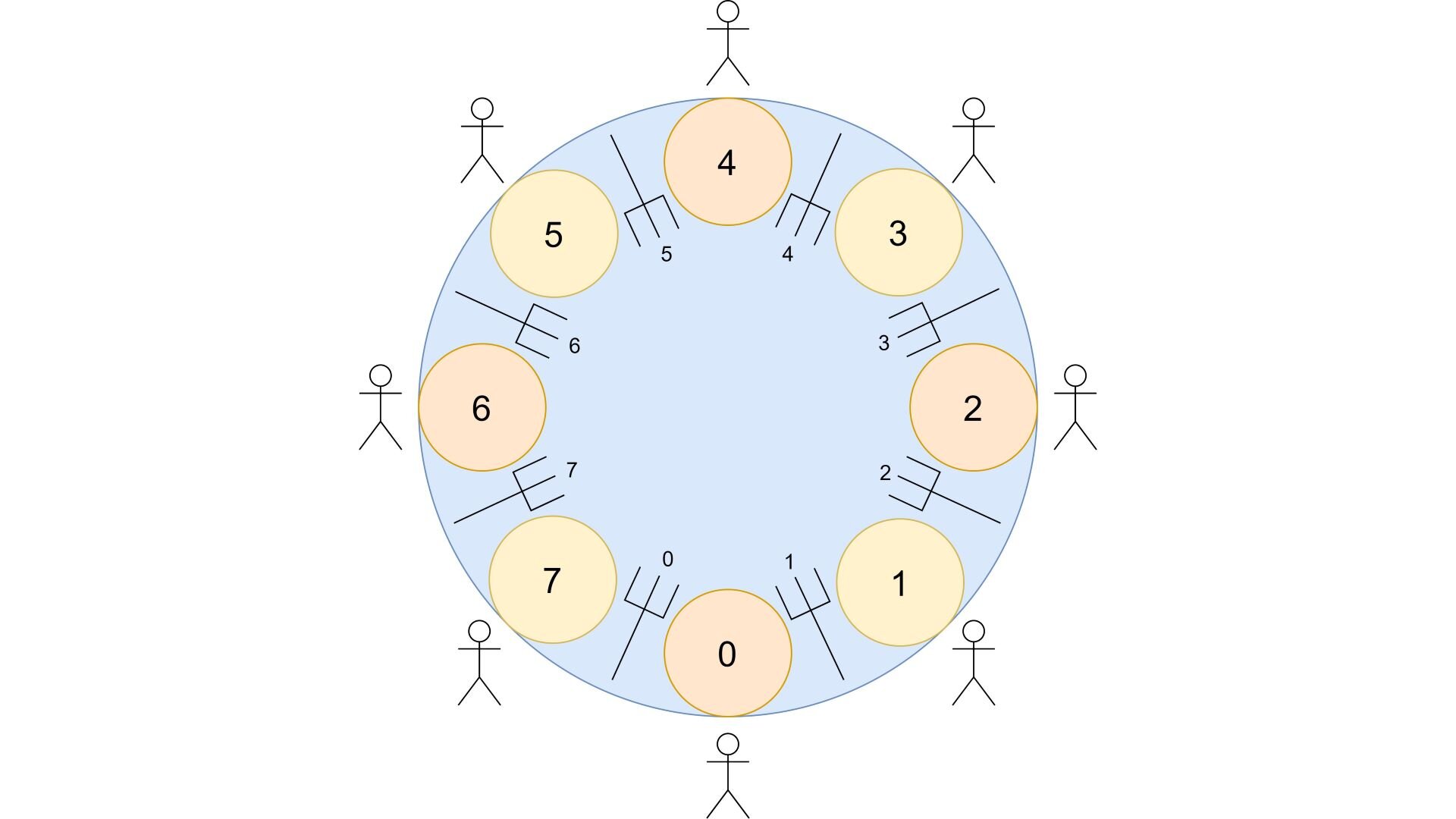
The dining philosophers problem is a well-known problem in computer science, originally formulated by Edsger Dijkstra to illustrate the possibility of deadlocks in programs where multiple threads lock and unlock multiple shared resources, such that a situation in which every thread is waiting for actions from other threads and no thread can thus continue it’s normal execution may occur. We will consider different approaches for solving this problem in the present post.
The singular matrix decomposition plays a major role in linear algebra and has a lot of applications, including lossy image compression. In this post we will discuss it in the context of the mentioned image compression with the focus on the intuition behind the algorithm, without going deep into the theory.