Computing square roots modulo a prime with the Tonelli-Shanks algorithm

15.09.2022 in Mathematics → Algebra, Cryptography Last modified at: 18.02.2023

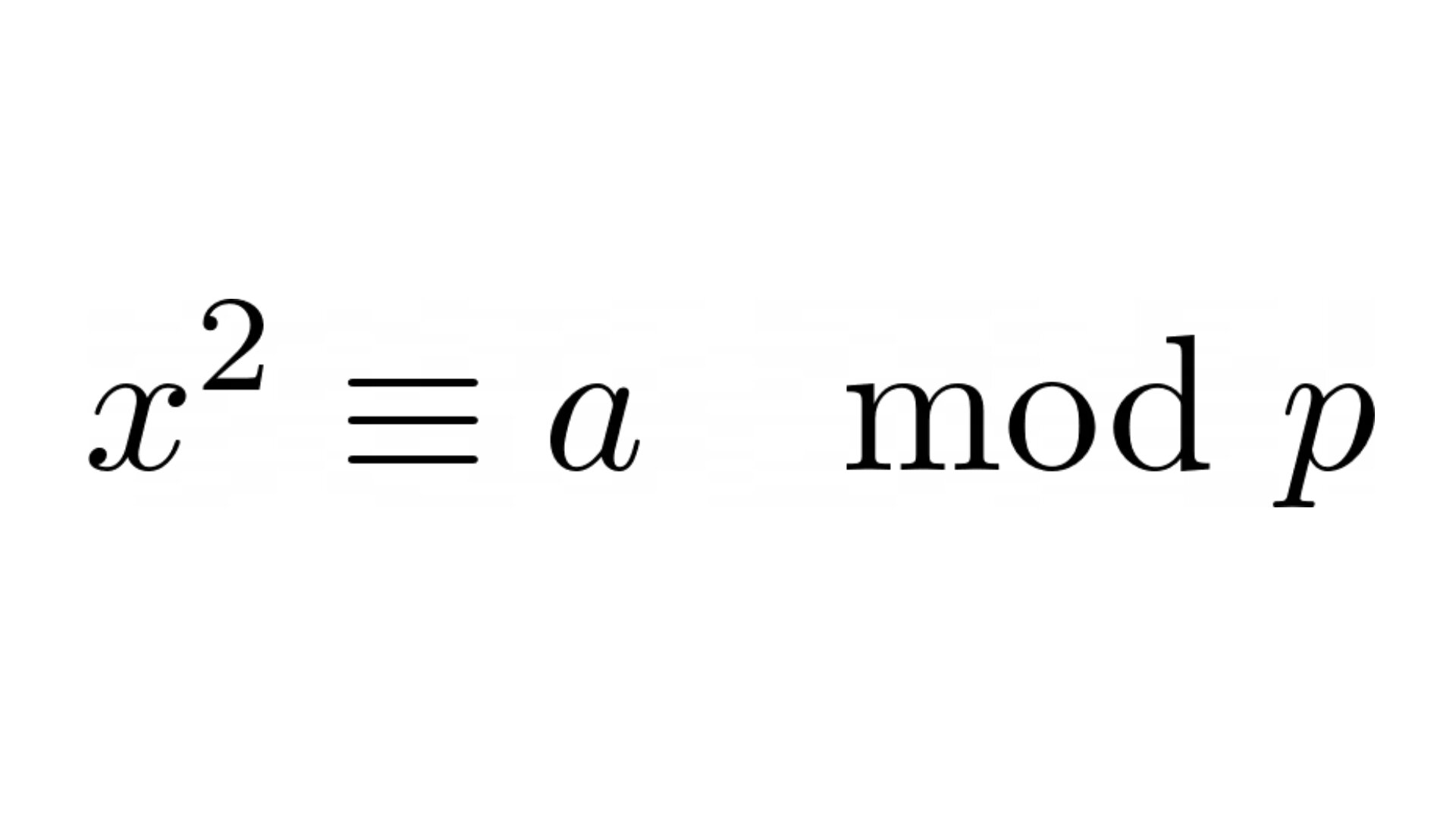
This post is about the problem of computing square roots modulo a prime number, a well-known problem in algebra and number theory. Nowadays multiple highly-efficient algorithms have been developed to solve this problem, e.g. Tonelli-Shanks, Cipolla’s algorithms. In this post we will focus on one of the most prominent algorithms, namely the Tonelli-Shanks algorithm, which is often described in a rather complicated way in the literature, although its derivation and the idea behind it is actually simple and elegant. The goal of this post is to showcase this beauty of the theory and to then show how the Tonelli-Shanks algorithm can be implemented in Python. We also discuss some interesting connections of this problem to cryptography.

Preliminaries

Formally, the problem of computing square roots modulo a prime is to solve the congruence $b^2 \equiv a \mod p$

for $b$, given an odd prime number $p$ and $a \in (\mathbb{Z}/p\mathbb{Z})^*$, which is also called a quadratic residue if the congruence above holds. We first discuss some theory we will rely on in the next section about the Tonelli-Shanks algorithm itself.

Let $q_p$ be the squaring endomorphism defined as follows $\begin{aligned} q_p : (\mathbb{Z}/p\mathbb{Z})^* &\rightarrow (\mathbb{Z}/p\mathbb{Z})^* \\ a &\mapsto a^2 \end{aligned}$

(recall that an endomorphism is a homomorphism of an algebraic structure to itself, it is an easy exercise to verify that $q_p$ is indeed an endomorphism). Observe that $\ker(q_p) = \{1, -1\}$, because every element of the kernel is a root of the $x^2 - 1 = (x - 1) \cdot (x + 1)$ polynomial, which cannot have more than two roots because of its degree, meaning that $1$ and $-1$ are its only roots. Let $Q_p := \operatorname{im}(q_p) = \{x^2 \mid x \in (\mathbb{Z}/p\mathbb{Z})^*\}$

be the set of all squares modulo $p$. In the following lemma, we derive a formula for the exact number of squares modulo $p$:

Lemma: Let $p$ be an odd prime. Then $\st Q_p\st = \frac{p-1}{2}$.

Proof: By the fundamental homomorphism theorem, there exists an isomorphism $(\mathbb{Z}/p\mathbb{Z})^* / \ker(q_p) \cong \operatorname{im}(q_p) = Q_p$

Since all cosets have equal cardinality, $\st Q_p\st = \st \operatorname{im}(q_p)\st = \frac{\st (\mathbb{Z}/p\mathbb{Z})^*\st}{\st \ker(q_p)\st} = \frac{p - 1}{2}$

This completes the proof.

Another major tool for characterizing squares modulo $p$ is the Legendre symbol defined as follows $\Big(\frac{a}{p}\Big) := \begin{cases} 0 & a \equiv 0 \mod p \\ 1 & a \not\equiv 0 \mod p \text{ and } a \text{ is a square modulo } p \\ -1 & \text{otherwise} \end{cases}$

where $a \in \mathbb{Z}$ and $p$ is a prime. If $a \in (\mathbb{Z}/p\mathbb{Z})^*$, then we can think of $\big(\frac{a}{p}\big)$ as of an “indicator” variable outputting $1$ if $b^2 \equiv a \mod p$ holds for some $b$ and $-1$ otherwise. In fact, the Legendre symbol can be computed efficiently via the Euler’s criterion formulated in the following theorem.

Theorem (Euler): Let $a \in \mathbb{Z}$ and $p$ is an odd prime. Then: $\Big(\frac{a}{p}\Big) \equiv a^{\frac{p-1}{2}} \mod p$

Proof: If $a \equiv 0 \mod p$, then the statement holds trivially. We thus focus only on the case when $a \in (\mathbb{Z}/p\mathbb{Z})^*$. By Fermat’s little theorem, it holds that $\Big(a^{\frac{p-1}{2}}\Big)^2 \equiv a^{p-1} \equiv 1 \mod p$

which is equivalent to $\Big(a^{\frac{p-1}{2}}\Big)^2 - 1 \equiv 0 \mod p$

meaning that $\Big(a^{\frac{p-1}{2}} - 1\Big) \cdot \Big(a^{\frac{p-1}{2}} + 1\Big) \equiv 0 \mod p$

Since we are working over the finite field $\mathbb{Z}/p\mathbb{Z}$, there cannot exist non-trivial divisors of zero, so it follows that $a^{\frac{p-1}{2}} \in \{1, -1\}$ modulo $p$. Thus, the following mapping $\begin{aligned} \varphi : (\mathbb{Z}/p\mathbb{Z})^* &\rightarrow (\{1, -1\}, \cdot) \\ a &\mapsto a^{\frac{p-1}{2}} \end{aligned}$

is a well-defined homomorphism of groups. Moreover, $\varphi$ is actually an epimorphism (i.e, is a surjective homomorphism), which can be shown as follows:

• $1 \in \operatorname{im}(\varphi)$, because $\varphi(1) = 1$.

• $-1 \in \operatorname{im}(\varphi)$, because $(\mathbb{Z}/p\mathbb{Z})^*$ is a cyclic group meaning that its generator $g$ cannot have order less than $\st (\mathbb{Z}/p\mathbb{Z})^*\st = p - 1$. Thus, $1 \neq \varphi(g) \in \{1, -1\} = \operatorname{im}(\varphi)$, so it follows that $\varphi(g) = -1$.

In other words, we have just shown that $\st \operatorname{im}(\varphi)\st = 2$. At this point, to prove the theorem it suffices to show that $\ker(\varphi) = Q_p$. The inclusion $\ker(\varphi) \supseteq Q_p$ is easy: if $a \in Q_p$, i.e., $a \equiv b^2 \mod p$, then $\varphi(a) = a^{\frac{p-1}{2}} = \big(b^2\big)^{\frac{p-1}{2}} = b^{p-1} = 1$

where all computations are modulo $p$ and the last equality holds by Fermat’s little theorem. With $\ker(\varphi) \supseteq Q_p$ proven, since we are working over the finite field $\mathbb{Z}/p\mathbb{Z}$ it suffices to show that $\st \ker(\varphi)\st = \st Q_p\st$ in order to prove that $\ker(\varphi) = Q_p$. By the previous lemma, $\st Q_p\st = \frac{p-1}{2}$, so it suffices to prove that $\st \ker(\varphi)\st = \frac{p-1}{2}$. Indeed, since by the fundamental homomorphism theorem $(\mathbb{Z}/p\mathbb{Z})^* / \ker(\varphi) \cong \operatorname{im}(\varphi)$

and all cosets are of equal cardinality, $\frac{\st (\mathbb{Z}/p\mathbb{Z})^*\st}{\st \ker(\varphi)\st} = \st \operatorname{im}(\varphi)\st = 2$

Solving for $\st \ker(\varphi)\st$ yields $\st \ker(\varphi)\st = \frac{\st (\mathbb{Z}/p\mathbb{Z})^*\st}{\st \operatorname{im}(\varphi)\st} = \frac{p-1}2{} = \st Q_p\st$

This completes the proof. Having done this preparatory work, we now discuss and implement the Tonelli-Shanks algorithm.

Computing square roots modulo a prime

First observe that since $p$ is a prime, $\mathbb{Z}/p\mathbb{Z}$ is a field and hence the polynomial $x^2 - a$ has exactly two roots. It follows that it suffices to compute just one root of $a$, because it is trivial to obtain the other one by simply performing negation modulo $p$. From now on, all computation will be modulo $p$ if not stated otherwise. We also assume that $a \in (\mathbb{Z}/p\mathbb{Z})^*$, or, equivalently, that $a \neq 0$, because it is trivial to compute the square root of zero.

The core idea behind the Tonelli-Shanks algorithm is to make use of the fact that if $a^m = 1$ for some odd $m \in \mathbb{N}$, then $\Big(a^{\frac{m+1}{2}}\Big)^2 = a^{m+1} = a$

and hence $a^{\frac{m+1}{2}}$ is a square root of $a$. By the Euler’s theorem of the previous section above, we know that $a^{\frac{p-1}{2}} = 1$ holds if and only if $a$ is a square modulo $p$: if $a^{\frac{p-1}{2}} = -1$, then the algorithm can directly identify that the given number is not a square and terminate accordingly. Thus, intuitively $m = \frac{p-1}{2}$ is a “good” initial value to start with while searching for an odd $m \in \mathbb{N}$ satisfying $a^m = 1$. The remaining ideas are best shown by looking at how the algorithm works on a concrete example.

Example

Let $p = 17$ and $a = 8$. $a \in Q_p$, because $(\frac{a}{p}) = a^{\frac{p-1}{2}} = a^8 = 1$. We set $m := \frac{p-1}{2} = 8$. Unfortunately, we cannot compute the square root of $a$ directly using the $a^{\frac{m+1}{2}}$ formula above, because $m$ is even. We thus divide $m$ by $2$ as long as possible and hope that at some point $m$ will become odd such that $a^m = 1$ still holds:

$m$	$\frac{p-1}{2} = 8$	$\frac{p-1}{4} = 4$
$a^m$	$1$	$-1$

Unfortunately, already after the first division of $m$ by two we get $a^m = a^4 = -1$, but we want to have one on the right-hand side. The idea is to pick some $b \in (\mathbb{Z}/p\mathbb{Z})^* \setminus Q_p$, because by Euler’s Theorem (see above) $b^{\frac{p-1}{2}} = \Big(\frac{b}{p}\Big) = -1$

It thus holds that $1 = \underbrace{a^m}_{-1} \cdot \underbrace{b^{\frac{p-1}{2}}}_{-1} = a^{\frac{p-1}{4}} \cdot b^{\frac{p-1}{2}} = \big(a \cdot b^2\big)^m$

Let $b := 3 \in (\mathbb{Z}/p\mathbb{Z})^* \setminus Q_p$. We now run the algorithm recursively to compute the square root of $a_2 := a \cdot b^2 = 8 \cdot 9 = 4$, because then we can recover the square root of $a$ by multiplying the square root of $a_2$ with $b^{-1}$. We repeatedly divide $m$ by two and recompute $a_2^m$ in the same way we did above:

$m$	$\frac{p-1}{4} = 4$	$\frac{p-1}{8} = 2$
$a_2^m$	$1$	$-1$

Again, already after the very first division of $m$ by two we obtain $-1$. We thus again write $1 = \underbrace{a_2^m}_{-1} \cdot \underbrace{b^{\frac{p-1}{2}}}_{-1} = a_2^{\frac{p-1}{8}} \cdot b^{\frac{p-1}{2}} = \big(a_2 \cdot b^4\big)^m$

and determine recursively the square root of $a_3 := a_2 \cdot b^4 = 1$:

$m$	$\frac{p-1}{8} = 2$	$\frac{p-1}{16} = 1$
$a_3^m$	$1$	$1$

We now finally have the desired situation that $m = 1$ is odd and $a_3^m = 1$, so we can compute one of the square roots of $a_3$: $\sqrt{a_3} := a_3^{\frac{m+1}{2}} = a_3^{\frac{1+1}{2}} = a_3 = 1$

We now recall that $a_3 = a_2 \cdot b^4$, so it follows that the square root of $a_2$ is $\sqrt{a_2} := \sqrt{a_3} \cdot b^{-2} = 1 \cdot 3^{-2} = 2$

Similarly, since $a_2 = a \cdot b^2$, it follows that $\sqrt{a} = \sqrt{a_2} \cdot b^{-1} = 2 \cdot 3^{-1} = 2 \cdot 6 = 12$

Hence, the square roots of $a = 8$ modulo $p = 17$ are $\pm 12$, that is, $5$ and $12$.

The Tonelli-Shanks algorithm

We now state the Tonelli-Shanks algorithm in general:

1. Set $m := \frac{p-1}{2}$. If $a^m = -1$, then return “not a square”, because $a$ is not a square modulo $p$ by Euler’s theorem (see above) and $a^m$ is equal to the Legendre symbol.

2. Otherwise we have that $a^m = 1$. Set $k := 1$, so that $m = \frac{p-1}{2^k}$

3. At this point we have the invariant that $a^m = 1$ for $m = \frac{p-1}{2^k}$. While $m$ is even and $a^m = 1$, set $k := k + 1$ and update $m := \frac{p-1}{2^k}$.

4. If $a^m = 1$, then the square root of $a$ is $a^{\frac{m+1}{2}}$ by the above discussion, since $m$ is odd.

5. Otherwise it holds that $a^m = -1$ for $m = \frac{p-1}{2^k}$, where $k \ge 2$. Choose an arbitrary non-square $b \in (\mathbb{Z}/p\mathbb{Z})^* \setminus Q_p$ by repeatedly picking $b \in (\mathbb{Z}/p\mathbb{Z})^*$ uniformly at random until $(\frac{b}{p}) = b^{\frac{p-1}{2}} = -1$.

6. Run the same algorithm recursively from step 3 with the variable $a$ set to $a' := a \cdot b^{2^{k-1}}$ and other variables left unchanged. This establishes the invariant of step 3, because

$\begin{aligned} 1 = \underbrace{a^m}_{-1} \cdot \underbrace{b^{\frac{p-1}{2}}}_{-1} = \underbrace{a^{\frac{p-1}{2^k}}}_{-1} \cdot \underbrace{b^{\frac{p-1}{2}}}_{-1} &= a^{\frac{p-1}{2^k}} \cdot \Big(b^{2^{k-1}}\Big)^{\frac{p-1}{2^k}} \\ &= \Big(a \cdot b^{2^{k-1}}\Big)^{\frac{p-1}{2^k}} = \Big(\underbrace{a \cdot b^{2^{k-1}}}_{a'}\Big)^m \end{aligned}$

• Let $\sqrt{a'}$ be the square root of $a'$ obtained from the recursive call. We are interested in computing $\sqrt{a}$ such that $(\sqrt{a})^2 = a$ (interpret $\sqrt{a'}$ and $\sqrt{a}$ as new variables, not as operations). Observe that

$\big(\sqrt{a'}\big)^2 = a' = a \cdot b^{2^{k-1}} = (\sqrt{a})^2 \cdot b^{2^{k-1}}$

• Bringing $(\sqrt{a})^2$ to the left side yields

$(\sqrt{a})^2 = \big(\sqrt{a'}\big)^2 \cdot b^{-2^{k-1}} = \Big(\sqrt{a'} \cdot b^{-2^{k-2}}\Big)^2$

• Note that we have used the fact that $k \ge 2$ here. It follows that $\sqrt{a'} \cdot b^{-2^{k-2}}$ is a square root of $a$ modulo $p$.

We now argue why this algorithm always terminates and is correct. Observe that $m$ is changed throughout the algorithm in a way which ensures that $a^m \in \{1, -1\}$ always holds. This is the case, because $1, -1$ are the only square roots of $1$ modulo $p$ and in every step we divide the exponent $m$ only by two. The case when $a^m = -1$ is reduced to the case when $a^m = 1$ but for a different $a$, such that the square root for the original $a$ can be recovered from the square root of the new $a$. Finally, observe that the algorithm either terminates directly because $a^m = 1$ holds for an odd $m$, or $k$ gets increased by at least one and hence $m$ gets divided by a power of two greater than one. This guarantees termination, because iterative division of $m$ by two will at some point yield an odd number whereupon the algorithm will terminate.

We now make a few additional remarks about the Tonelli-Shanks algorithm.

• If $\frac{p-1}{2}$ is odd or, equivalently, if $p \equiv 3 \mod 4$, then the algorithm will not make any recursive calls and output the square root $a^{\frac{m+1}{2}} = a^{\frac{p+1}{4}}$ of $a$.

• The loop in step 3 of the algorithm can be optimized by replacing it with a binary search algorithm for finding an $m$ such that $a^m = -1$. If during such binary search, we have $a^m = 1$, then we continue searching for smaller values of $m$. If $a^m \notin \{1, -1\}$, then this means that we have divided $m$ too many times, so it follows that binary search is to be continued for larger values of $m$. Although this optimization is beautiful theoretically, in practice it may only give a very tiny performance gain, if any.

• The non-square $b$ used in the algorithm needs to be found and computed only once. During every recursive call, the same value of $b$ can be reused to deal with the $a^m = -1$ situation. This implies that $b^{-1}$ needs to be computed only once, so the computation of the $\sqrt{a'} \cdot b^{-2^{k-2}}$ value can be optimized.

• As regards the expected time needed to find a non-square $b$ via guessing, since exactly half of the elements of $(\mathbb{Z}/p\mathbb{Z})^*$ are non-squares, two is the expected number of times we need to generate $b$ uniformly at random and to test whether it is a non-square or not.

• The expected running time of the algorithm is $O(\log(p)^2)$, if we assume that multiplication modulo $p$ is a constant-time operation.

Implementation in Python

In this section I would like to show how the Tonelli-Shanks algorithm discussed above can be implemented in Python. We will need the following utility algorithms:

• The extended Euclidean algorithm for computing inverses modulo $p$

• Fast exponentiation (by squaring) algorithm

I will reuse the implementation of the extended Euclidean algorithm I described and proved correct in this post. We are now ready to dive into the code:

# file: "tonellishanks.py"
import random


def power_modulo(a: int, b: int, n: int) -> int:
    """ Computes a ^ b mod n """
    result = 1
    while b != 0:
        if b % 2 == 1:
            # b odd
            result = (result * a) % n
        a = (a * a) % n
        b >>= 1
    return result


def extended_gcd(a: int, b: int) -> (int, int, int):
    # optional check
    if a == 0:
        return b, 0, 1

    # without this check the first iteration will divide by zero
    if b == 0:
        return a, 1, 0

    un_prev = 1
    vn_prev = 0
    un_cur = 0
    vn_cur = 1

    while True:
        qn = a // b
        new_r = a % b
        a = b
        b = new_r

        if b == 0:
            return a, un_cur, vn_cur

        # Update coefficients
        un_new = un_prev - qn * un_cur
        vn_new = vn_prev - qn * vn_cur

        # Shift coefficients
        un_prev = un_cur
        vn_prev = vn_cur
        un_cur = un_new
        vn_cur = vn_new


def inverse_modulo(a: int, n: int) -> int:
    _, b, _ = extended_gcd(a, n)
    return b % n


def legendre_symbol(a: int, p: int, /) -> int:
    return power_modulo(a, (p - 1) >> 1, p)


def _choose_b(p: int, /) -> int:
    b = 2
    while legendre_symbol(b, p) == 1:
        b = random.randrange(2, p)
    return b


def _tonelli_shanks_recursive(a: int, k: int, p: int, b: int, b_inverse: int, /):
    """
    Computes a square root of a modulo prime p
    :param a: the number to take the square root of
    :param k: positive integer, such that a^m = 1 (mod p) where m = (p-1)/(2^k)
    :param p: odd prime p modulo which we are working
    :param b: an arbitrary non-square modulo p
    :param b_inverse: the inverse of b modulo p, i.e., b * b_inverse = 1 (mod p)
    :return: one of the square roots of a modulo p (the other can be obtained via negation modulo p)
    """

    m = (p - 1) >> k
    a_m = 1

    while m % 2 == 0 and a_m == 1:
        m >>= 1
        k += 1
        a_m = power_modulo(a, m, p)

    if a_m == p - 1:
        # a^m = -1 (mod p)
        b_power = 1 << (k - 1)
        b_power_half = 1 << (k - 2)
        a_next = (a * power_modulo(b, b_power, p)) % p
        a_next_root = _tonelli_shanks_recursive(a_next, k, p, b, b_inverse)
        a_root = a_next_root * power_modulo(b_inverse, b_power_half, p)
        return a_root % p

    # we now handle the case when m is odd
    # this case is easy, a^((m+1)/2) is a square root of a
    return power_modulo(a, (m + 1) >> 1, p)


def tonelli_shanks(a: int, p: int, /) -> int | None:
    """
    Computes a square root of a modulo prime p
    :param a: the number to take the square root of
    :param p: odd prime p modulo which we are working
    :return: one of the square roots of a modulo p (the other can be obtained via negation modulo p)
    """

    if legendre_symbol(a, p) != 1:
        # a is not not a square modulo p
        return None

    b = _choose_b(p)
    b_inverse = inverse_modulo(b, p)
    return _tonelli_shanks_recursive(a, 1, p, b, b_inverse)

Recall that performing a left bitwise shift (<<) is essentially a fast way to multiply the left operand with two raised to the right operand value’s power. Similarly, a right bitwise shift (>>) divides the left operand by two raised to the right operand value’s power.

Running the implementation on the example of the previous section, that is, for $a = 8$ and $p = 17$ yields the expected correct roots:

$ python3 -i tonellishanks.py
>>> tonelli_shanks(8, 17)
5
>>> tonelli_shanks(8, 17)
12

Note: The above implementation is a simplified version of my thoroughly tested implementation of the algorithm available in this GitHub repository.

Related hard problems

I find the problem of computing square roots modulo a prime especially interesting because it is in some sense very “close” to problems where there are very good reasons to believe that they are hard in the complexity-theoretic sense. For example, the same problem is not known to be efficiently solvable if we are working modulo a Blum number, that is, if we are interested in solving $b^2 \equiv a \mod p \cdot q$

for $b$, where $p \neq q$ are prime numbers such that $p \equiv q \equiv 3 \mod 4$. Moreover, this modified problem is at least as hard as the problem of factoring Blum numbers, because given an oracle for computing the four square roots for $a$, one could factor a given Blum number $n = p \cdot q$ efficiently as follows:

1. Choose a number $x \in (\mathbb{Z}/n\mathbb{Z})^*$ uniformly at random (can be implemented by simply choosing a random number $x$ between $2$ and $n - 1$ inclusively, because if $x \notin (\mathbb{Z}/n\mathbb{Z})^*$, then we have already effectively guessed the factor $1 < \gcd(x, n) < n$ of $n$)

2. Use the (hypothetical) oracle to compute some square root $r$ of $x^2$ modulo $n$.

3. If $r \equiv x \mod n$ or $r \equiv -x \mod n$, then we have failed to factor $n$.

4. Otherwise it holds that $(r - x) \cdot (r + x) \equiv 0 \mod n$ and the factors of $n$ are $\gcd(r - x, n)$ and $\gcd(r + x, n)$.

Since $x \in (\mathbb{Z}/n\mathbb{Z})^*$ is chosen at random and we only pass $x^2$ to the oracle, the oracle’s answer is independent of $x$. It is not hard to show that every quadratic residue modulo a Blum number has exactly 4 distinct roots (using the Chinese Remainder Theorem), two of them are $x$ and $-x$ which do not yield a factor of $n$ in the algorithm above. It follows that the probability of successfully factoring a number is $1/2$, meaning that the algorithm above is a randomized polynomial-time Turing reduction. Moreover, the success probability of the above algorithm can actually be significantly amplified, but this is outside of the scope of this post. It is also worth noting that the above security reduction is useful in cryptography. For example, the Rabin cryptosystem’s security heavily relies on the assumption that computing square roots modulo a Blum number is computationally hard, which as we have shown above is implied by the assumption that factoring Blum numbers is hard, which is a plausible hardness assumption to date. If Rabin’s cryptosystem did all computations modulo a prime instead of a Blum number, then the cipher would be easily breakable, since it would then be possible to decrypt plaintexts using the Tonelli-Shanks algorithm.