Constructing Hilbert-style F0 proofs with a simple graph-based notation
There exist different kinds of deductive systems in logic. Every deductive system consists of certain axioms and rules of inference. The problem of constructing a proof in every such system is quite difficult — computationally it is -Hard, since satisfiability can be reduced to it. So it is a good idea to trade-off between logical axioms and inference rules. Hilbert (Frege)-style proof systems are interesting because most of them use several axioms but only one inference rule — modus ponens, unlike, for example, Gentzen natural deduction. In other words, Hilbert-style proof systems “push” all the complexity of constructing a proof into the axioms — it is hard to syntactically instantiate them, but once done it is easier to combine them as there is only one rule of inference — modus ponens. In this post, I will present a notation for these Hilbert-style proofs I came up with recently, that allows one to construct them in a more systematic way, with less “guessing”.
The F0 Hilbert-style proof system
First, we need to define the proof system in which we will construct proofs. We will consider only formulas over without true and false. By the way, this is a complete operator set, so every boolean function can be expressed only by using negation and implication. Let
be the set of axioms, that hold for arbitrary propositional formulas , , and .
The only inference rule we need is modus ponens (MP), which can be defined as follows:
It can be proven that this is a sound and complete proof system.
Deduction theorem
In order to considerably simplify the proof construction in many cases, we need to briefly define the deduction theorem, which states that:
This theorem essentially provides a bridge between syntactic entailment and provability in the F0 proof system — for example, proving is equivalent to proving . Intuitively, this theorem holds because is valid and F0 is sound and complete.
The deduction theorem is not a rule of inference or an axiom — if some F0 proof uses it, then there exists a proof without it (this can be proven by induction).
Notation for proofs
Usually, proofs are defined as finite sequences of propositional formulas, where each element is either an axiom or modus ponens applied to some already proven formulas (that are located before the current formula in the sequence). For example, a typical proof of would be:
- — Axiom 1
- — Axiom 2
- — MP(1, 2)
- — Axiom 1
- — MP(4, 3)
However, such proofs are hard to construct by hand, because we need to come up with concrete instances of axioms and it isn’t trivial in many cases which formulas should be substituted for variables. It is therefore much easier to construct the proof in a bottom-up manner, which means that we start with the formula to be proven and then apply axioms, lemmas and modus ponens backwards.
For example, we can rewrite the proof above with the following graph notation:
In this notation:
- Nodes mean proven statements.
- Edge means that statement is needed for the proof of statement in one step — application of an axiom/lemma/assumption combined with modus ponens or simply modus ponens.
- Cycles are not allowed, because we cannot refer to the correctness of some statement while proving it (the graph is a DAG).
By the way, this notation is more compact compared to the list-notation because when applying an axiom, lemma or an assumption we don’t need to state it and then add the result of modus ponens. Instead of that, we just replace the left side of the axiom/lemma/assumption with it’s right side.
How to come up with F0 proofs
The intuitive “algorithm” for coming up with proofs in the F0 proof system can be summarized as follows:
- Apply the deduction theorem as much as possible.
- Derive as many formulas as possible from the assumptions.
- If the statement isn’t already proven, start constructing the proof bottom-up and apply axioms, lemmas, and assumptions as well as modus ponens backwards.
While performing the bottom-up construction of the proof, our goal is essentially to reach an already proven statement or an assumption from the statement to be proven. In order to do so, we need to iteratively search for ancestor nodes of some node that will get us closer to the desired assumptions or lemmas. For the construction of some node such that holds, we have the following options:
- Add an assumption or an already proven statement to the left of (see, for example, the above proof where the first construction step was to add to the left of ). This step is essentially modus ponens applied backwards.
- Let be the left-hand side of some assumption or already proven statement if is an instance of it’s right-hand side (see, for example, how Axiom 2 was applied above).
Examples
In the following examples, different F0 proofs are visualized with the graph notation described above. It is also a good idea to read these proofs bottom-up, this is how I constructed them.
Lemma 1 (Trivial implication)
Proof: The statement follows directly with the deduction theorem. Also, we already proved this statement above without using the deduction theorem.
Lemma 2 (Double negation elimination)
Proof: By the deduction theorem, the above statement is equivalent to
Lemma 3 (Introduce double negation)
Proof:
Lemma 4 (Double negation implication)
Proof: By the deduction theorem, the above statement is equivalent to
Lemma 5 (Implication transitivity 1)
Proof: By the deduction theorem, the above statement is equivalent to
Lemma 6 (Simple implication transitivity)
Proof: By the deduction theorem, the above statement is equivalent to
Lemma 7 (Implication transitivity 2)
Proof: By the deduction theorem, the above statement is equivalent to
Lemma 8 (Implication from inconsistency)
Proof: By the deduction theorem, the above statement is equivalent to
Lemma 9 (Implication from contradiction)
Proof: By the deduction theorem, the above statement is equivalent to
Lemma 10
Proof: By the deduction theorem, the above statement is equivalent to
Lemma 11 (Contraposition)
Proof: By the deduction theorem, the above statement is equivalent to
Lemma 12 (Elimination of assumptions)
Proof: By the deduction theorem, the above statement is equivalent to
Lemma 13
Proof: By the deduction theorem, the above statement is equivalent to
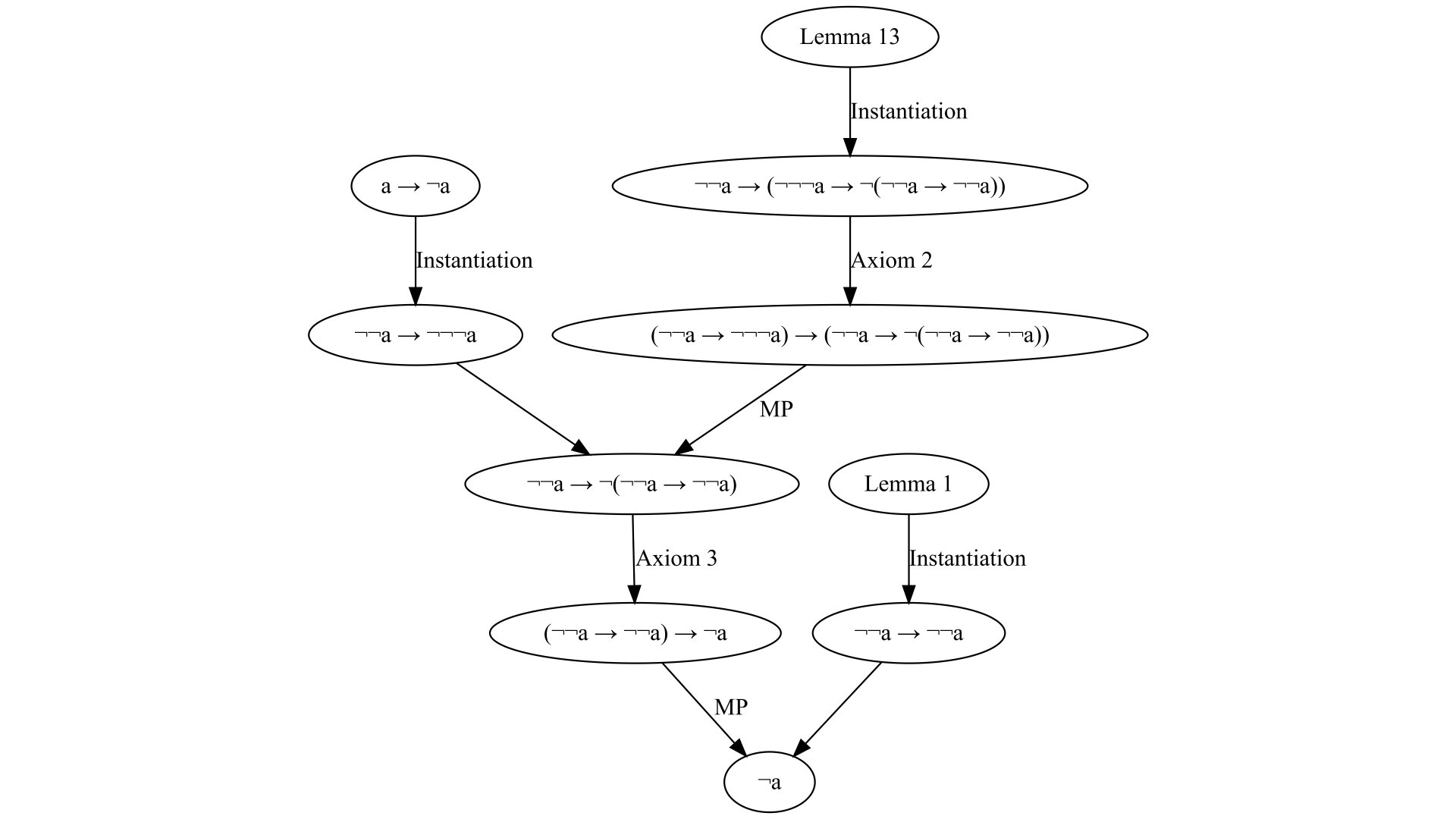
Lemma 14
Proof: By the deduction theorem, the above statement is equivalent to
Lemma 15 (Proof by contradiction)
Proof: By the deduction theorem, the above statement is equivalent to














