Knuth-Morris-Pratt (KMP) algorithm explained

20.12.2020 in Computer Science

Almost every program has to somehow process and transform strings. Very often we want to identify some fixed pattern (substring) in the string, or, formally speaking, find an occurrence of $\beta := b_0b_1 \dots b_{n-1}$ in $\alpha := a_0a_1 \dots a_{m-1} \neq \varepsilon$. A naive algorithm would just traverse $\alpha$ and check if $\beta$ starts at the current character of $\alpha$. Unfortunately, this approach leads us to an algorithm with a complexity of $O(n \cdot m)$. In this post we will discuss a more efficient algorithm solving this problem - the Knuth-Morris-Pratt (KMP) algorithm.

The Knuth-Morris-Pratt algorithm

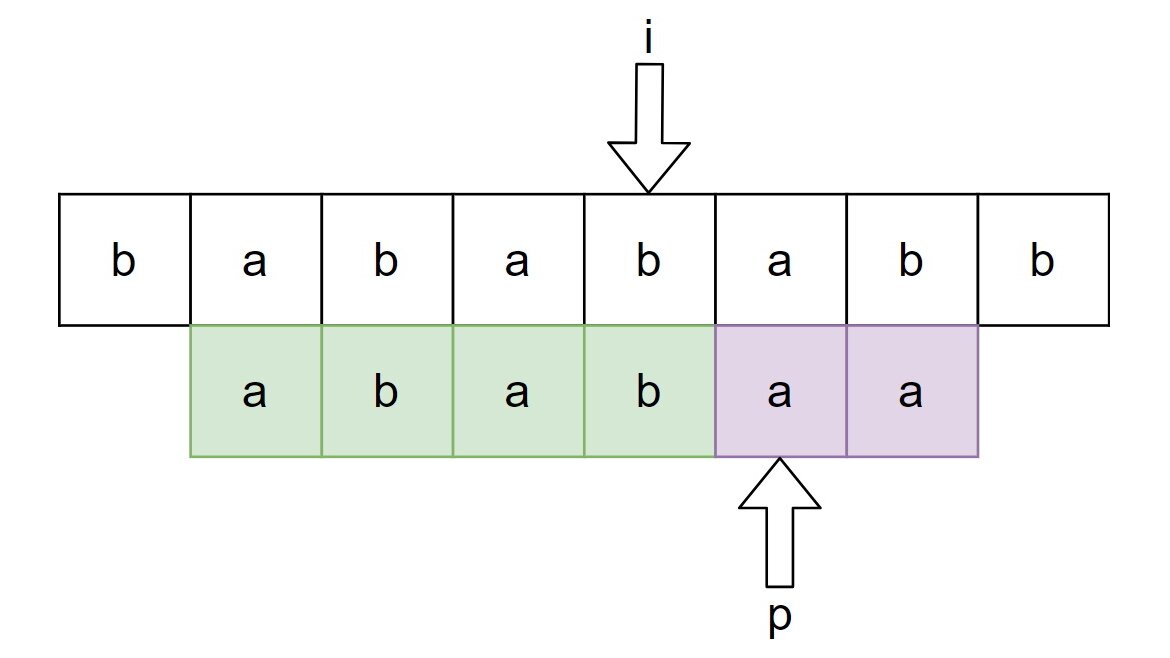
Obviously, the substring search algorithm has to somehow compare both strings character-after-character. Suppose we are scanning the string from left to right and we found $b_0$. Then we can start comparing further characters of $\beta$ with the next characters of $\alpha$. If the remaining characters match, we’ve found an occurrence of $\beta$ in $\alpha$. So the key question is what the algorithm should do if there is a mismatch during this comparison process, as shown in this example:

If the characters we are currently comparing don’t match, then we need to somehow shift the green, “matching” area of $\beta$. This green area that we expand if the characters match and shift otherwise is often referred to as the window. If we found a mismatch, it is possible that some suffix of the window together with the current character form a prefix of $\beta$, so we must shift the window so that this prefix of $\beta$ ends at the current position. In the example above, we must shift the window by 5 characters to the right so that the arrow denoting the current position points at the first character b of the window.

Or, for example, in this situation

we should shift the window by 2 characters to the right and get:

The current elements (above the arrow) match so we can proceed by comparing further characters. By the way, it is important to shift only by 2 characters and not by 4, because otherwise it is possible that we skip too many characters and don’t detect a valid occurrence of $\beta$ in $\alpha$.

To generalize and formalize how we shift the window when the current characters don’t match, we will define the so-called failure function:

Let $f(j)$ be the length of the longest proper prefix of $b_0b_1 \dots b_j$, such that this prefix is also a suffix of $b_0b_1 \dots b_j$. In this context, proper means that it is not the string itself so the prefix is not trivial.

The idea behind the failure function is that when we find mismatching characters while comparing the window with $\alpha$, we should shift the window such that the $f(i)$-th character of the window is at the position of the last character $i$ of the window (green area). In other words, the window should be shifted by $w - f(i)$ characters to the right, where $w$ is the size of the window. If, after shifting the window, there is still a mismatch, then it is possible that there is a shorter suffix that matches some prefix of $b_0 \dots b_i$ so we need to repeat the process again.

With this idea and assuming the failure function is computed and stored in the f array, we can implement the Knuth-Morris-Pratt algorithm the following way:

# returns the index of the first occurrence of b in a
def kmp(a: str, b: str, f: list) -> int:
    
    m = len(a)
    assert m >= 1
    n = len(b)
    p = 0
    
    for i in range(m):
        
        while p != 0 and a[i] != b[p]:
            p = f[p - 1]
        
        if a[i] == b[p]:
            p += 1

        # invariant formally defined below
        assert a[i + 1 - p:i + 1] == b[0:p]

        if p == n:
            return i + 1 - n
    
    return -1 # no match found

Proof of correctness: To formally prove the correctness of the above program, we will define the following invariant which is also verified with the assert statement in code: After every iteration of the for loop, before the last if statement, it holds that $a_{i+1-p} \dots a_i = b_0 \dots b_{p-1}$. Intuitively, it means that the window is correct:

Induction base: We excluded the case $\alpha = \varepsilon$ in the formal definition of the problem, so the loop will be entered. On the first iteration, the window is empty ($p = 0$) and the while loop will not be entered because we don’t need to shift the empty window. If the first characters match, then $p$ will be incremented establishing the invariant. Otherwise, the window will remain empty.

Induction step: By induction hypothesis, we assume that the invariant holds for some $i$ and $p$. If $p = n$, it means that $a_{i+1-n} \dots a_i = b_0 \dots b_{n-1} = \beta$, so we found an occurrence of $\beta$ in $\alpha$ at the position $i + 1 - n$, and the algorithm terminates. If this is not the case and there is a further character in $\alpha$, we enter a new iteration of the loop and shift the window by $p - f(p - 1)$ characters on the right by assigning p to point to the $f(p - 1)$ character of the string. Intuitively by doing this we shift the window so that the new window is the greatest possible proper prefix of the old window, that is also it’s suffix. For this reason it is guaranteed that the window remains valid and we only need to compare the current elements: If a[i] != b[i], then it means that the prefix we took is probably too large and we should search for a smaller one by repeating the window shifting step, until we either find a match or $p$ becomes zero meaning that the window is empty. The body of the if statement after the loop expands the window in case the current characters match, establishing the invariant.

It is also important to note, that the window should be shifted by $p - f(p - 1)$ characters to the right, because if we take some shorter prefix that is also a suffix of $b_0 \dots b_{p - 1}$, it is possible that we don’t detect an occurrence of $\beta$ in $\alpha$. This completes the proof.

In the example above, the window gets shifted by $p - f(p - 1) = 5 - f(4) = 5 - 3 = 2$ characters to the right, $i$ gets incremented and the window gets expanded (by incrementing $p$) because a[i] == b[p]:

Computing the failure function

An important part of the KMP algorithm is, of course, the computation of the failure function we defined above. We can come up with an efficient algorithm computing it by approaching the problem with dynamic programming. Suppose we want to compute $f(n - 1)$ and we already computed $f(i)$ for all $0 \le i \le n - 2$. The value of $f(n - 2)$ gives us the length of the longest suffix ending at $b_{n-2}$ such that there is a corresponding prefix of this length (equal parts of the string are visualized with braces): $\beta = \underbrace{b_0 \dots b_{f(n-2)-1}}_{f(n-2)} b_{f(n-2)} \dots b_{n-2-f(n-2)} \underbrace{b_{n-1-f(n-2)} \dots b_{n-2}}_{f(n-2)} b_{n-1}$

By the way, is is possible that the parts of the formula marked with braces intersect, because there is no guarantee that $f(n-2) - 1 < n - 1 - f(n-2) \Leftrightarrow f(n-2) < \frac{n}{2}$.

If the characters after the equal parts in braces are also the same, or, formally, if $b_{f(n-2)} = b_{n-1}$, then we can conclude that $f(n-1) = f(n-2) + 1$.

If $b_{f(n-2)} \neq b_{n-1}$, then the longest prefix of $\beta$ that is also it’s suffix must have length $k \le f(n-2)$. Suppose we found such maximum $k < f(n-2)$ such that: $\begin{aligned} b_0 \dots b_{k-1} &= b_{n-1-k} \dots b_{n-2} \\ \underbrace{\overbrace{b_0 \dots b_{k-1}}^{k} b_{k} \dots b_{f(n-2)-1}}_{f(n-2)} &= \underbrace{b_{n-1-f(n-2)} \dots b_{n-2-k} \overbrace{b_{n-1-k} \dots b_{n-2}}^{k}}_{f(n-2)} \end{aligned}$

Then, by combining these equations, it follows that there must be a suffix of length $k$ equal to the prefix of $b_0 \dots b_{k-1} b_{k} \dots b_{f(n-2)-1}$

So, the maximum possible suffix that is also a prefix has length $k := f(n-2)$, if $b_k = b_{n-1}$. We can apply this important fact we derived multiple times — if $b_k \neq b_{n-1}$, then the maximum suffix/prefix we are searching for has length $l := f(k - 1)$, if $b_l = b_{n-1}$, and so on.

The base case for the dynamic programming approach is simple: $f(0) = 0$, because the only proper prefix of $b_0$ is the empty string $\varepsilon$.

We are now ready to implement the computation of the failure function:

def compute_f(b):

    n = len(b)
    f = [0]

    for i in range(1, n):
        
        k = f[i - 1]
        
        while k != 0 and b[i] != b[k]:
            k = f[k - 1]

        if b[i] == b[k]:
            k += 1

        f.append(k)  # f[i] = k

    return f

In the case of a mismatch the while-loop searches for potential shorter suffix, that is also a prefix of $\beta$. If it was found, then the loop terminates with $k$ representing the first character after the prefix. If the loop terminated because of $k = 0$, then it means that there is no shorter prefix that is also a suffix (it is empty), so the value of the failure function is either 0 or 1, depending on whether the current character is equal to the first one.

Of course, we can run the functions above and check the result:

a = "baabbbaabbaabbbabaabbbaabaabababba"
b = "baababa"
print("a:", a)
print("b:", b)
f = compute_f(b)
print("Failure function:")
print("i   :", [i for i in range(len(b))])
print("f(i):", f)  # [0, 0, 0, 1, 2, 1, 2]
found = kmp(a, b, f)
print("Result:", found)  # 24

Finding all matches

The Knuth-Morris-Pratt algorithm can be easily extended to detect all occurrences of $\beta$ in $\alpha$:

def kmp(a: str, b: str, f: list) -> list:

    m = len(a)
    assert m >= 1
    n = len(b)
    p = 0

    matches = []

    for i in range(m):
        
        while p != 0 and a[i] != b[p]:
            p = f[p - 1]
        
        if a[i] == b[p]:
            p += 1

        if p == n:
            matches.append(i + 1 - n)
            p = f[p - 1]
    
    return matches

If the window has length $n$ and we thus found an occurrence of $\beta$ in $\alpha$, all we need to do is to shift the window by $n - f(n - 1)$ characters to the right. We need to do it in the body of the if p == n: statement, because the while loop expects that the window is a proper prefix of $\beta$ and thus $p$ is a valid index.

Complexity analysis

It may seem that both the computation of the failure function as well as the matching itself have a complexity of $\Theta(n \cdot m)$ because of the 2 nested loops in both algorithms. However, this is not the case. We can first show, that the failure function can be computed in linear time:

Failure function computation complexity

We’ve already argued above that $f(i) \le f(i - 1) + 1 \quad\forall i \in \{1, \dots, n - 1\}$ and $f(0) = 0$. It follows, that $f(i) \le i$ also holds for all $0 \le i < n$. Because of that, during a single iteration of the for loop, the while loop makes at most $k$ iterations where $k$ is the initial value of the k variable.

We will now prove that the body of of the while loop (in particular, the k = func[k - 1] statement) gets executed at most $n$ times during the entire algorithm: the maximum value of $k$ is $n - 1$, so if the while loop is entered, then it will make at most $n - 1$ iterations and because $f(i) \le f(i - 1) + 1$, the value of $k$ will decrease by at least the amount of iteration of the while loop.

Therefore, the overall running time of the algorithm is in $O(n)$.

Matching algorithm complexity

Assuming the failure function is computed and stored in an array so that the access time is constant, the complexity of the Knuth-Morris-Pratt algorithm is $O(m)$. The proof of this fact is analogous to the previous proof.