Implementing and visualizing Gram-Schmidt orthogonalization

19.02.2021 in Computer Science → Linear algebra Last modified at: 20.02.2021

In linear algebra, orthogonal bases have many beautiful properties. For example, matrices consisting of orthogonal column vectors (a. k. a. orthogonal matrices) can be easily inverted by just transposing the matrix. Also, it is easier for example to project vectors on subspaces spanned by vectors that are orthogonal to each other. The Gram-Schmidt process is an important algorithm that allows us to convert an arbitrary basis to an orthogonal one spanning the same subspace. In this post, we will implement and visualize this algorithm in 3D with a popular Open-Source library manim.

Gram-Schmidt process

Consider some arbitrary $d$-dimensional subspace $A = \langle a_1, \dots, a_d \rangle$

spanned by linear independent vectors $a_1, \dots, a_d$. We want to find the following basis spanning the same subspace: $A = \langle q_1, \dots, q_d \rangle$

The Gram-Schmidt process is a typical dynamic programming algorithm, because the core idea behind it is to make $\langle q_1, \dots, q_i \rangle$ an orthogonal basis assuming $\langle q_1, \dots, q_{i-1} \rangle$ is already such a basis. The construction works as follows:

Step 1: For $q_1$, we can just take $a_1$ and normalize it: $q_1 := \frac{a_1}{\lVert a_1 \rVert}$

Step 2: $q_2$ must be orthogonal to $\langle q_1 \rangle$, so we need to find out the component of $a_2$ that is orthogonal to $\langle q_1 \rangle$. We can do this by subtracting the projection of $a_2$ onto $\langle q_1 \rangle$ from $a_2$: $q'_2 := a_2 - \frac{(q_1^\top a_2) q_1}{q_1^\top q_1} = a_2 - (q_1^\top a_2) q_1$

The second equality holds because we normalized the $q_1$ vector and the denominator is thus equal to one.

This step can be visualized as follows:

Finally, we need to normalize the resulting vector: $q_2 := \frac{q'_2}{\lVert q'_2 \rVert}$

Step 3: $q_3$ must be orthogonal to $\langle q_1, q_2 \rangle$, which is already an orthogonal basis, so $q_3$ must be orthogonal to both $\langle q_1 \rangle$ and $\langle q_2 \rangle$ which means that we need to subtract the projections of $a_3$ onto both $\langle q_1 \rangle$ and $\langle q_2 \rangle$ from $a_3$: $q'_3 := a_3 - (q_1^\top a_3) q_1 - (q_2^\top a_2) q_2$

As in the previous step, we normalize the vector: $q_3 := \frac{q'_3}{\lVert q'_3 \rVert}$

More generally, we can write the formulas for step $1 \le i \le d$ as follows:

Step i: $q_i$ must be orthogonal to $\langle q_1, \dots, q_{i-1} \rangle$. Because in the previous steps we made $\langle q_1, \dots, q_{i-1} \rangle$ an orthogonal basis, it follows that $q_i$ must be orthogonal to each vector from $\{q_j : j < i\}$. We therefore subtract projections of $a_i$ onto $q_j$ for all $j < i$ from $a_i$: $q'_i := a_i - (q_1^\top a_i) q_1 - (q_2^\top a_i) q_2 - \dots - (q_{i-1}^\top a_i) q_{i-1}$

Now we only need to normalize the new basis vector: $q_i := \frac{q'_i}{\lVert q'_i \rVert}$

Implementation & Visualization

We can implement the Gram-Schmidt orthogonalization algorithm in Python the following way:

import numpy as np


def gram_schmidt(A):
    
    (n, m) = A.shape
    
    for i in range(m):
        
        q = A[:, i] # i-th column of A
        
        for j in range(i):
            q = q - np.dot(A[:, j], A[:, i]) * A[:, j]
        
        if np.array_equal(q, np.zeros(q.shape)):
            raise np.linalg.LinAlgError("The column vectors are not linearly independent")
        
        # normalize q
        q = q / np.sqrt(np.dot(q, q))
        
        # write the vector back in the matrix
        A[:, i] = q

The input basis vectors are given as columns of the matrix, which then get’s modified in-place by the algorithm. It is important to verify that $q'_i$ is not zero, because if $q'_i = 0$, then it means that $a_i \in \langle q_1, \dots, q_{i-1} \rangle = \langle a_1, \dots, a_{i-1} \rangle$ and $\langle a_1, \dots, a_d \rangle$ is therefore not a basis (vectors are not linearly independent).

In order to visualize the algorithm, I added a few yield-statements to the above implementation, because they allow us to elegantly separate the algorithm from the code visualizing it. For the visualization itself, I will use the popular manim library:

# file: "gram-schmidt.py"
from manimlib.imports import *
from enum import Enum


class Action(Enum):
    UPDATE_MATRIX_REMOVE_Q = 1
    ADD_PROJECTION = 2
    REMOVE_PROJECTIONS_SET_Q = 3
    NORMALIZE_Q = 4


def gram_schmidt(A):
    
    (n, m) = A.shape
    
    for i in range(m):
        
        q = A[:, i] # i-th column of A
        
        for j in range(i):
            yield (Action.ADD_PROJECTION, np.dot(A[:, j], A[:, i]) * A[:, j])
            q = q - np.dot(A[:, j], A[:, i]) * A[:, j]
        
        if np.array_equal(q, np.zeros(q.shape)):
            raise np.linalg.LinAlgError("The column vectors are not linearly independent")
        
        yield (Action.REMOVE_PROJECTIONS_SET_Q, q)
        
        # normalize q
        q = q / np.sqrt(np.dot(q, q))

        yield (Action.NORMALIZE_Q, q)
        
        # write the vector back in the matrix
        A[:, i] = q

        yield (Action.UPDATE_MATRIX_REMOVE_Q, None)


class GramSchmidt(ThreeDScene):

    CONFIG = {
        "x_axis_label": "$x$",
        "y_axis_label": "$y$",
        "basis_i_color": GREEN,
        "basis_j_color": RED,
        "basis_k_color": GOLD,
        "q_color": PURPLE,
        "q_shifted_color": PINK,
        "projection_color": BLUE
    }

    def create_matrix(self, np_matrix):

        m = Matrix(np_matrix)

        m.scale(0.5)
        m.set_column_colors(self.basis_i_color, self.basis_j_color, self.basis_k_color)

        m.to_corner(UP + LEFT)

        return m

    def construct(self):
        
        M = np.array([
            [1.0, 1.0, -3.0],
            [3.0, 2.0, 1.0],
            [-2.0, 0.5, 2.5]
        ])

        axes = ThreeDAxes()

        axes.set_color(GRAY)

        axes.add(axes.get_axis_labels())

        self.set_camera_orientation(phi=55 * DEGREES, theta=-45 * DEGREES)

        basis_helper = TextMobject("$ a_1 $", ",", "$ a_2 $", ",", "$ a_3 $")
        basis_helper[0].set_color(self.basis_i_color)
        basis_helper[2].set_color(self.basis_j_color)
        basis_helper[4].set_color(self.basis_k_color)

        q_helper = TextMobject("Current $ q_i $ vector")
        q_helper[0].set_color(self.q_color)

        q_shifted_helper = TextMobject("Shifted $ q_i $ vector")
        q_shifted_helper[0].set_color(self.q_shifted_color)

        projection_helper = TextMobject("Projection vectors")
        projection_helper[0].set_color(self.projection_color)

        helper = VGroup(
            projection_helper,
            q_helper,
            q_shifted_helper,
            basis_helper
        )

        helper.arrange(
            DOWN,
            aligned_edge = RIGHT,
            buff=0.1
        )

        helper.to_corner(UP + RIGHT)

        self.add_fixed_in_frame_mobjects(helper)

        # matrix

        matrix = self.create_matrix(M)

        self.add_fixed_in_frame_mobjects(matrix)

        # axes & camera

        self.add(axes)

        self.begin_ambient_camera_rotation(rate=0.15)

        i_vec = Vector(M[:, 0], color=self.basis_i_color)
        j_vec = Vector(M[:, 1], color=self.basis_j_color)
        k_vec = Vector(M[:, 2], color=self.basis_k_color)

        self.play(
            GrowArrow(i_vec),
            GrowArrow(j_vec),
            GrowArrow(k_vec),
            Write(helper)
        )

        self.wait()

        projection_vectors = []

        q = None

        for (action, payload) in gram_schmidt(M):

            if action == Action.UPDATE_MATRIX_REMOVE_Q:

                assert not q is None

                M_rounded = np.round(M.copy(), 2)
                
                self.remove(matrix)

                matrix = self.create_matrix(M_rounded)

                self.add_fixed_in_frame_mobjects(matrix)

                i_vec_new = Vector(M[:, 0], color=self.basis_i_color)
                j_vec_new = Vector(M[:, 1], color=self.basis_j_color)
                k_vec_new = Vector(M[:, 2], color=self.basis_k_color)

                animation_time = 2.0

                self.play(
                    FadeOut(q, run_time=animation_time * 0.75),
                    ReplacementTransform(i_vec, i_vec_new, run_time=animation_time),
                    ReplacementTransform(j_vec, j_vec_new, run_time=animation_time),
                    ReplacementTransform(k_vec, k_vec_new, run_time=animation_time)
                )

                self.wait()

                i_vec, j_vec, k_vec = i_vec_new, j_vec_new, k_vec_new

            elif action == Action.ADD_PROJECTION:

                p = Vector(payload, color=self.projection_color)

                projection_vectors.append(p)

                self.play(GrowArrow(p))

                self.wait()

                if len(projection_vectors) == 2:

                    first_projection_end = projection_vectors[0].get_end()

                    p_shifted = Arrow(first_projection_end, first_projection_end + payload, buff=0, color=self.projection_color)

                    projection_vectors[1] = p_shifted

                    self.play(ReplacementTransform(p, p_shifted))

                    self.wait()

            elif action == Action.REMOVE_PROJECTIONS_SET_Q:

                if not projection_vectors:

                    q = Vector(payload, color=self.q_color)

                    self.play(GrowArrow(q))

                    self.wait()

                    continue

                last_projection_end = projection_vectors[len(projection_vectors) - 1].get_end()

                q_shifted = Arrow(last_projection_end, last_projection_end + payload, buff=0, color=self.q_shifted_color)

                self.play(GrowArrow(q_shifted))

                self.wait()

                q = Vector(payload, color=self.q_color)

                self.play(
                    ReplacementTransform(q_shifted, q),
                    *[FadeOut(p) for p in projection_vectors]
                )

                self.wait()

                projection_vectors = []

            elif action == Action.NORMALIZE_Q:

                q_normalized = Vector(payload, color=self.q_color)

                self.play(ReplacementTransform(q, q_normalized))

                self.wait()

                q = q_normalized

            else:
                assert False

            self.wait(1)

        assert np.allclose(M.T @ M, np.identity(3))

        self.wait(15)

By rendering the animation with manim gram-schmidt.py GramSchmidt -m -p, we get:

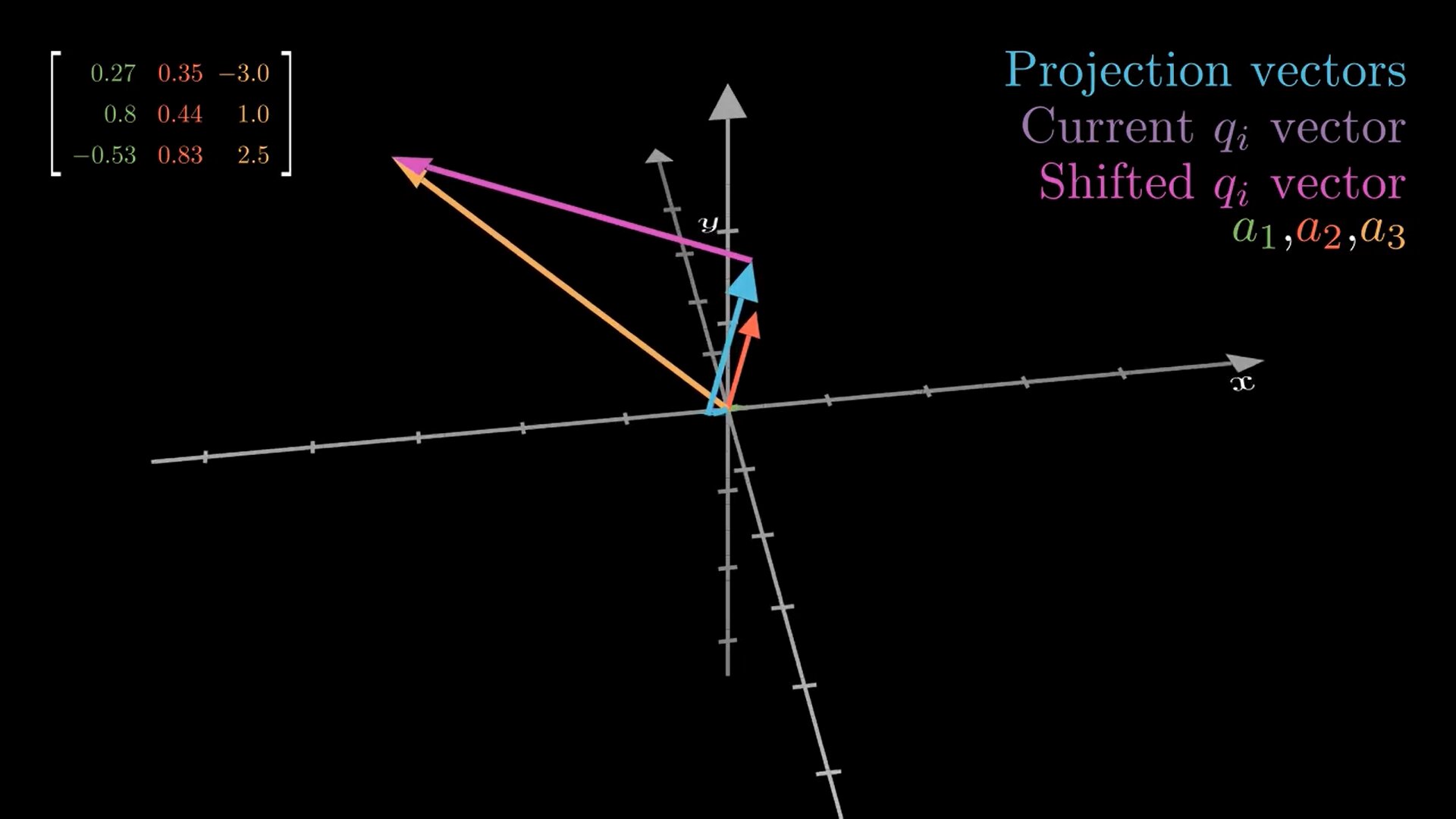
Vector colors in the animation mean the following:

• The green, red and gold vectors are initially the $a_1$, $a_2$ and $a_3$ vectors, respectively. During the algorithm they get iteratively replaced by the $q_i$-vectors, so that at the end these vectors represent $q_1$, $q_2$ and $q_3$, respectively (as we can see, they are orthogonal to each other at the end).
• The blue vectors are the projections of $a_i$ onto $q_j$, $j < i$.
• The pink vector is the shifted $q'_i$ vector at step $i$.
• The purple vector is the $q'_i$ vector at step $i$ (pink vector moved to the origin). This vector then gets normalized.