Efficient algorithm for finding non-productive rules in context-free grammars

17.04.2021 in Computer Science → Research Last modified at: 28.04.2021

In programs that somehow deal with context-free grammars automatically, we may want to check whether some part of the grammar “makes sense” and isn’t totally redundant and useless. In other words, we may want to check whether some non-terminal or production can come up in some arbitrary sentential form. This problem arises often when the program we are implementing accepts user-defined grammars. In this post, we will consider an existing algorithm that solves the problem as well as introduce and implement a new, more efficient algorithm that detects useless parts of an input grammar.

The problem

Consider a context-free grammar $G = (\mathcal{N}, \mathcal{T}, \mathcal{P}, S)$, where $\mathcal{N}$ is the set of non-terminals, $\mathcal{T}$ is the set of terminals, $\mathcal{P}$ is the set of productions and $S \in \mathcal{N}$ is the starting symbol.

Let us call a production $A \rightarrow \gamma$ productive iff $\gamma \Rightarrow^* \alpha$ holds for some $\alpha \in \mathcal{T}^*$. In other words, it is always possible to derive at least one word from a productive production. We call a production unproductive or non-productive iff it is not productive. For example, the following grammar with starting symbol $S$ $\begin{aligned} S &\rightarrow A c D \mid \varepsilon \\ A &\rightarrow B b \\ B &\rightarrow C \\ C &\rightarrow a A \\ D &\rightarrow d \end{aligned}$

has only 2 productive rules: $S \rightarrow \varepsilon$ and $D \rightarrow d$. This is the case because non-terminals $A$, $B$, and $C$ derive each other in a cycle.

Productive productions are exactly the productions that we can use when constructing a parse tree for some arbitrary word, since if we reduce a production that itself cannot derive any word, the parse tree will at that point become either infinite or we will not be able to apply any further rules and parsing will therefore fail. Because of this, it is always a good idea to remove unproductive productions from the grammar before trying to parse some word — the language defined by the grammar will not change. But how do we detect such useless and redundant productions?

Closure algorithm

The problem we just defined is typically solved with a closure algorithm. The idea is inductive:

Base: Any production $A \rightarrow \alpha$ where $\alpha$ is a word (sequence of terminals, including $\alpha = \varepsilon$) is a productive production, because a word can be derived directly in one derivation step. Also, $A$ is a productive non-terminal, which analogously means that we can derive some word from $A$.

Step: For every $A \rightarrow \alpha \in \mathcal{P}$, if $\alpha$ consists only of terminals or productive non-terminals, then $A$ is also a productive non-terminal and $A \rightarrow \alpha$ is a productive rule.

We can start with $P_0$ and $\begin{aligned} P_0 &= \{A \rightarrow \alpha \in \mathcal{P} \mid \alpha \in \mathcal{T}^*\} \\ P_1 &= \{A \rightarrow \alpha \in \mathcal{P} \mid \alpha \in (\mathcal{T} \cup \{B \in \mathcal{N} \mid B \rightarrow \beta \in P_0\})^*\} \\ \vdots \\ P_{i + 1} &= \{A \rightarrow \alpha \in \mathcal{P} \mid \alpha \in (\mathcal{T} \cup \{B \in \mathcal{N} \mid B \rightarrow \beta \in P_i\})^*\} \end{aligned}$

compute $P_i$ iteratively for $i = 0,1,2,\dots$ until $i = j \in \mathbb{N}$ such that $P_{j-1} = P_j$. Intuitively, this simply means that we apply the step described above until no more productive rules are found.

The downside of such an algorithm is its complexity: even if we implement the algorithm in a way that allows us to check in constant time whether a certain non-terminal is productive according to the current step, we still need to iterate over all productions to find the ones with the right side consisting only of terminals or already productive non-terminals. Each step has therefore complexity in $\Omega(\st\mathcal{P}\st)$ which means that the overall worst-case complexity is in $\Omega(\st \mathcal{P} \st \cdot \st \mathcal{N} \st)$, because in the following worst-case scenario the algorithm will make $\Theta(\st \mathcal{N} \st)$ iterations: $\begin{aligned} A_1 &\rightarrow A_2 \\ A_2 &\rightarrow A_3 \\ &\vdots \\ A_k &\rightarrow a \end{aligned}$

Designing a more efficient algorithm

The above algorithm is not efficient because it detects only one new unproductive non-terminal in each step in the worst case. In order to optimize it, we need to somehow analyze the structure of the grammar to directly detect how the productivity of some rules affects the productivity of other ones. More precisely, the algorithm needs to be able to efficiently detect non-productive loops as shown in the example at the beginning of this post, non-terminals that cannot be reached from the start symbol as well as how one rule directly affects the productivity of another rule. The core idea is the following:

Lemma: For every production $P := A \rightarrow \alpha_1 B_1 \dots \alpha_{n-1} B_k \alpha_n$ where $n \in \mathbb{N}^+, k \in \mathbb{N}_0$, $\alpha_i \in \mathcal{T}^*$, $B_i \in \mathcal{N}$, this production $P$ is productive if and only if $B_1, \dots, B_k$ are all productive. If $P$ is productive, then $A$ is productive as well.

Proof: The correctness of this lemma follows directly from the definition of productivity.

Now, we want to come up with a data structure that captures all grammar rules and makes it easy for an algorithm to apply the above statement — we need to analyze the nature of how exactly the lemma above links productivity of rules. Also, we need to keep in mind that the data structure must be able to express productivity of both productions and non-terminals.

Some non-terminal is productive iff all non-terminals on the right side of at least one corresponding rule are productive. Intuitively, it means that for the left non-terminal, productivity can be expressed as a disjunction of conjunctions. This leads us to the idea that the data-structure could be something like an implication graph where sets of non-terminals are vertices and productions are edges. In such a graph, an edge $\{B_1, \dots, B_n\} \rightarrow^P \{A\}$ means that if $B_1, \dots, B_n$ are productive, then production $P$ and non-terminal $A$ are also productive.

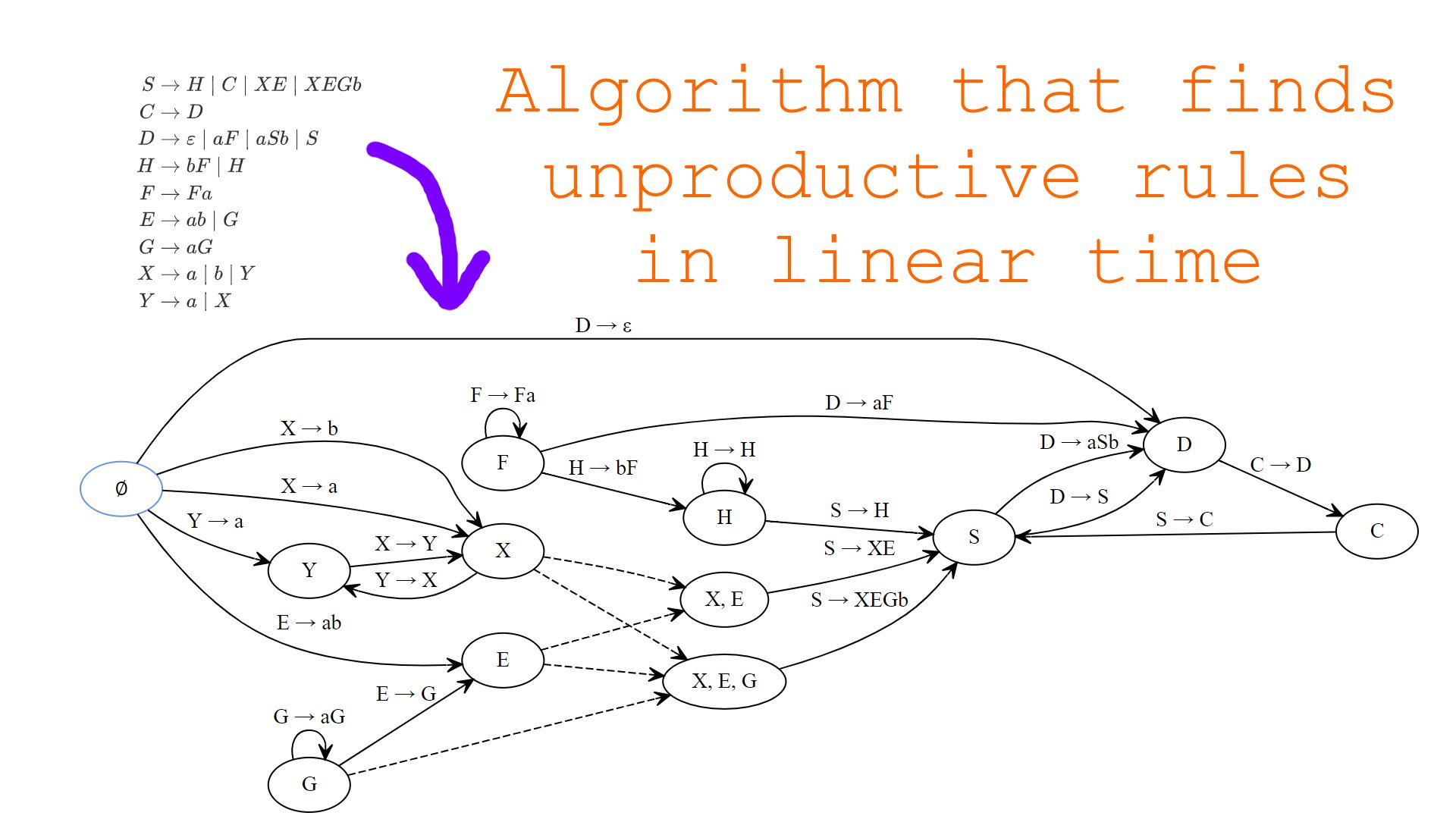
For example, consider the following grammar with starting symbol $S$: $\begin{aligned} S &\rightarrow H \mid C \mid X E \mid X E G b \\ C &\rightarrow D \\ D &\rightarrow \varepsilon \mid a F \mid a S b \mid S \\ H &\rightarrow b F \mid H \\ F &\rightarrow F a \\ E &\rightarrow a b \mid G \\ G &\rightarrow a G \\ X &\rightarrow a \mid b \mid Y \\ Y &\rightarrow a \mid X \end{aligned}$

By creating an edge $\{B_1, \dots, B_k\} \rightarrow^P \{A\}$ for each $P = A \rightarrow \alpha_1 B_1 \dots \alpha_{n-1} B_k \alpha_n$, we get the following multigraph that illustrates how the productivity of some non-terminals implies productivity of other non-terminals and productions:

In this multigraph, edges leaving $\varnothing$ are production edges where the production contains only terminals on the right side. By construction of the multigraph, going over a further edge is equivalent to applying the lemma above, hence all edges reachable from the $\varnothing$ node are productive. However, the converse is not yet true, because we need a way to visit nodes containing two or more non-terminals in case all single non-terminals have already been visited and are therefore productive.

To later implement such visiting efficiently, we can introduce a new type of edges — count-down edges. I will also call nodes that contain two or more non-terminals compound. The idea is the following: For each compound node, we can additionally store a counter that is initialized with the amount of non-terminals in that node. When a node containing a single non-terminal is visited, the counter for all compound nodes containing that node is decremented and if, after decrementing, it becomes zero, then the compound node can also be visited. In other words, when the counter of some compound node is zero, it means that all two or more non-terminals on the right of some production are productive and thus the production itself is productive. We can implement this count-down behavior by creating a count-down edge $B_i \rightarrow \{B_1, \dots, B_n\}$ for all $1 \le i \le n$:

Count-down edges in the multigraph essentially mean that some vertex can be visited only if all nodes required for visiting that node are already visited. Count-down edges work like AND-gates in digital circuits. For example, the following count-down edges simply mean, that node $\{A, B, C\}$ can be visited only after nodes $A$, $B$ and $C$ have all been visited:

By adding count-down edges (marked dashed) for each compound node to the multigraph for the above example grammar, we get the following final multigraph:

In this multigraph, productions reachable from the $\varnothing$ node are exactly the productive productions and nodes reachable from $\varnothing$ are exactly the productive nodes. Unproductive rules can be calculated trivially once we’ve calculated productive ones — they correspond to red edges that were not visited during the traversal of the multigraph:

The efficient algorithm

The above description of the algorithm is informal because I focused on the intuition and tried to explain how I came up with this algorithm. Now we can write it down formally and analyze it:

Input: Context-free grammar $G = (\mathcal{N}, \mathcal{T}, \mathcal{P}, S)$.

Output: Set $D \subseteq \mathcal{P}$ of non-productive rules.

Algorithm:

1. Initialize an empty directed multigraph $G = (V, E, s, t)$, where:
   • Vertices $V \subseteq 2^{\mathcal{N}}$ are sets of non-terminals.
   • Edges $E \subseteq \mathcal{P} \cup (\mathcal{N} \times2^{\mathcal{N}})$ are either productions or count-down edges.
   • The source of a production edge where $\alpha$ and $\beta$ are words is $s(A \rightarrow \alpha_1 B_1 \dots \alpha_{n-1} B_k \alpha_n) := \{B_1, \dots, B_k\}$
   • The target of a production edge is $t(A \rightarrow \alpha_1 B_1 \dots \alpha_{n-1} B_k \alpha_n) := \{A\}$.
   • The source of a count-down edge $s((n, N)) := \{n\}$ is a single non-terminal node.
   • The target of a count-down edge $t((n, N)) := N$ is a compound node.
2. For each $p := A \rightarrow \alpha_1 B_1 \dots \alpha_{n-1} B_k \alpha_n \in \mathcal{P}$ where $n \in \mathbb{N}^+$, $k \in \mathbb{N}_0$, $\alpha_i \in \mathcal{T}^*$, $B_i \in \mathcal{N}$:
   • Create an edge $p \in E$ as well as nodes $s(p)$ and $t(p)$ if they didn’t already exist.
   • If $k \ge 2$, then also create a count-down edge $e := (B_i, \{B_1, \dots, B_k\}) \in E$ for all $1 \le i \le k$. If $s(e)$ or $t(e)$ are missing in the graph, add them.
3. If $\varnothing \notin V$, terminate the algorithm with $D := \mathcal{P}$.
4. Let $c : \{A \in V \mid \st A \st \ge 2\} \rightarrow G$ be the counter — for all $A \in V$ with $\st A \st \ge 2$ initialize $c(A) := \st A \st$.
5. Let $P := \varnothing$ be the set of productive productions, initialized with the empty set.
6. Traverse the graph with depth first search starting at $\varnothing \in V$:
   • If a productive outgoing edge $e \in \mathcal{P}$ is detected, add $e$ to $P$ and push $t(e)$ onto the stack.
   • If a count-down outgoing edge $(n, N) \in \mathcal{N} \times2^{\mathcal{N}}$ is detected, set $c(N) := c(N) - 1$. If, after this decrement, $c(N) = 0$, push $t((n, N)) = N$ onto the stack.
7. Terminate the algorithm with $D := \mathcal{P} - P$.

This algorithm can also be tweaked a bit:

• Breadth first search can be used instead of depth first search.
• Unproductive non-terminals can be detected instead of unproductive rules — a non-terminal is productive if it was visited during the depth first search traversal. We can thus analogously build an algorithm that determines productive non-terminals.

Complexity analysis

For the complexity analysis, we will assume that the length of the productions is limited by some constant. This implies that every production can create only constant many nodes and edges in the multigraph and thus $\st V \st \in O(\st \mathcal{P} \st)$ and $\st E \st \in O(\st \mathcal{P} \st)$ hold.

• Step 2 has complexity $\Theta(\st \mathcal{P} \st)$.
• Steps 3 and 5 run in constant time.
• Step 4 runs in time in $O(\st \{A \in V \mid \st A \st \ge 2\} \st) \subseteq O(\st V \st) \subseteq O(\st \mathcal{P} \st)$.
• Step 6 has complexity $O(\st V \st + \st E \st) \subseteq O(\st \mathcal{P} \st + \st \mathcal{P} \st) = O(\st \mathcal{P} \st)$.
• Step 7 takes time in $O(\st \mathcal{P} \st)$.

The overall time complexity is therefore $O(\st \mathcal{P} \st) \subseteq o(\st \mathcal{P} \st \cdot \st \mathcal{N} \st)$ which means that this algorithm is more efficient compared to the closure approach that has worst-case complexity $\Omega(\st \mathcal{P} \st \cdot \st \mathcal{N} \st)$.

Space complexity of this algorithm is also $O(\st \mathcal{P} \st)$.

Implementation

I’ve implemented this algorithm in Rust, the complete source code can be found in this repository. Here, I will only focus on parts of the code that are most relevant for the algorithm and describe a small trick I used to reduce the amount of data structures the algorithm needs to maintain.

Our goal is to calculate the set of non-productive rules and for that we need the set of productive rules which is essentially the edges visited so far. Normally, in a depth first search, we track which vertices have already been visited, but in this algorithm we can reuse the set of productive rules to determine whether we already used that edge in the traversal. In the get_productive_productions function below, we therefore only check whether the edge has not yet been visited.

// file: "useless.rs"
use crate::grammar::{Symbol, Grammar, ProductionReference};
use std::collections::{HashMap, HashSet, BTreeSet};
use std::rc::Rc;

enum Edge {
    Production(ProductionReference),
    CountDown(BTreeSet<Rc<Symbol>>)
}

struct FindUselessProductions {
    graph: HashMap<BTreeSet<Rc<Symbol>>, Vec<Edge>>,
    starting_productions: HashSet<ProductionReference>
}

fn single_nonterminal_node(symbol: &Rc<Symbol>) -> BTreeSet<Rc<Symbol>> {
    let mut set = BTreeSet::new();
    set.insert(Rc::clone(symbol));
    set
}

impl FindUselessProductions {

    fn new() -> Self {
        Self {
            graph: HashMap::new(),
            starting_productions: HashSet::new()
        }
    }

    fn handle_production(&mut self, pr: ProductionReference) {

        let ProductionReference(label, body) = pr;

        let right_nonterminals = body
            .iter()
            .filter_map(|symbol| if symbol.is_nonterminal() {
                Some(Rc::clone(symbol))
            } else {
                None
            })
            .collect::<BTreeSet<_>>();

        // create node for the label of the current production if the node is not yet present
        self.graph
            .entry(single_nonterminal_node(&label))
            .or_insert_with(|| vec![]);

        if right_nonterminals.is_empty() {
            // this production contains only terminal symbols on its right hand side
            // it is therefore productive

            self.starting_productions.insert(ProductionReference(label, body));

            return;
        }

        if right_nonterminals.len() == 1 {
            let key = single_nonterminal_node(
                right_nonterminals.iter().next().unwrap()
            );

            self.graph
                .entry(key)
                .or_insert_with(|| vec![])
                .push(Edge::Production(ProductionReference(label, body)));

            return;
        }

        debug_assert!(right_nonterminals.len() >= 2);

        for nonterminal in right_nonterminals.iter() {
            debug_assert!(nonterminal.is_nonterminal());

            self.graph
                .entry(single_nonterminal_node(nonterminal))
                .or_insert_with(|| vec![])
                .push(Edge::CountDown(right_nonterminals.clone()));
        }

        self.graph
            .entry(right_nonterminals)
            .or_insert_with(|| vec![])
            .push(Edge::Production(ProductionReference(label, body)));
    }

    fn get_productive_productions(&self) -> HashSet<ProductionReference> {

        let mut stack = self.starting_productions
            .iter()
            .map(|pr| single_nonterminal_node(&pr.0))
            .collect::<Vec<_>>();

        let mut visited = self.starting_productions.clone();

        let mut counters = HashMap::new();

        while let Some(node) = stack.pop() {

            for edge in self.graph.get(&node).unwrap() {

                match edge {
                    Edge::Production(pr) => {

                        if !visited.contains(pr) {

                            visited.insert(pr.clone());

                            stack.push(single_nonterminal_node(&pr.0));

                        }

                    }
                    Edge::CountDown(symbols) => {

                        // countdown edges can only go from nodes containing
                        // single non-terminals
                        debug_assert!(node.len() == 1);
                        // countdown edges can only lead to nodes containing
                        // multiple symbols
                        debug_assert!(symbols.len() >= 2);

                        if !counters.contains_key(&node) {

                            let counter = counters
                                .entry(symbols.clone())
                                .or_insert_with(|| symbols.len());

                            debug_assert!(*counter >= 1);

                            *counter -= 1;

                            if *counter == 0 {
                                // this is the last remaining edge to a compound node
                                // we therefore go over this edge in our dfs

                                stack.push(symbols.clone());
                            }
                        }
                    }
                }

            }

            if node.len() == 1 {
                counters.insert(node.clone(), 0);
            }

        }

        visited
    }

    fn get_non_productive_productions(&self, grammar: &Grammar) -> HashSet<ProductionReference> {

        let productive_productions = self.get_productive_productions();

        let all_productions = grammar
            .all_productions()
            .collect::<HashSet<ProductionReference>>();

        all_productions
            .difference(&productive_productions)
            .map(|e| e.clone())
            .collect::<HashSet<ProductionReference>>()
    }

}

pub fn find_useless_productions(grammar: &Grammar) -> HashSet<ProductionReference> {
    let mut useless = FindUselessProductions::new();
    for pr in grammar.all_productions() {
        useless.handle_production(pr);
    }
    useless.get_non_productive_productions(grammar)
}

However, only checking if a productive edge has already been visited is not enough. If some node has an outgoing count-down edge and there exists a cycle out of production edges that leads back to that node, this node will be visited twice and the counter of the compound node will thus be decremented twice which means that a non-productive production may be marked by the algorithm as productive.

To avoid this bug, in the program above we use the counters hash-map for two purposes at the same time:

• To store the current value of the counter for a compound node.
• To mark a node containing a single non-terminal as visited after all its edges have been considered, in case there is an outgoing count-down edge.

A compound node cannot be visited twice because only count-down edges lead to them and we check whether a node with a single non-terminal has already been visited before decrementing the counter and possibly visiting a compound node.