Finding an injective mapping with restrictions for values is NP-Complete

07.08.2021 in Computer Science → Research, Complexity theory Last modified at: 04.09.2022

This post is about an interesting problem I recently tried to solve efficiently but ended up proving its NP-completeness. Informally, the problem is to find an injective mapping between two finite sets with certain, statically defined properties for values. For example, if $A = \{a, b, c, d\}$ and $B = \{1, 2, 3, 4, 5\}$, we may want to find an injective mapping $f : A \rightarrow B$ with restrictions $f(a) \in \{1, 3, 4, 5\}$, $f(b) \in \{3, 4, 5\}$, $f(c) \in \{1, 2, 4, 5\}$, $f(d) \in \{1, 2, 5\}$, $f(e) \in \{1, 2, 3, 4\}$. I find this problem of particular interest, because its nature is in my opinion very different compared to well-known NP-complete problems proven to be so by Karp. In this post we will visualize and formalize this problem, prove its NP-completeness and, finally, derive some interesting corollaries.

The problem

The above intuitive description of the problem can be equivalently formalized as follows:

Name: Restricted injective mapping

Input: A set $A$ as well as a collection $S = \{A_1, \dots, A_n\}$ of subsets of $A$, i.e. $A_i \subseteq A$ for all $1 \le i \le n$.

Question: $\exists (a_1, \dots, a_n) \in A_1 \times \dots \times A_n$ such that $a_i \neq a_j$ for all $i \neq j, 1 \le i,j \le n$?

This definition is equivalent to the brief description of the problem at the beginning of this post, since we can only focus on the restrictions in the target set (assuming that the elements in the source set are numbered) and it is possible to define such an injective mapping $f$​ if and only if $\exists (a_1, \dots, a_n) \in A_1 \times \dots \times A_n$​ such that $a_i \neq a_j$​ for all $i \neq j$​.

Example

Consider the following instance of the problem: $\begin{aligned} A &:= \{1, 2, 3, 4, 5, 6\} \\ A_1 &:= \{1, 3, 4, 5\} \\ A_2 &:= \{3, 4, 6\} \\ A_3 &:= \{1, 2, 4, 5\} \\ A_4 &:= \{1, 2, 5\} \\ A_5 &:= \{1, 2, 3, 4\} \\ S &:= \{A_1, A_2, A_3, A_4, A_5\} \end{aligned}$

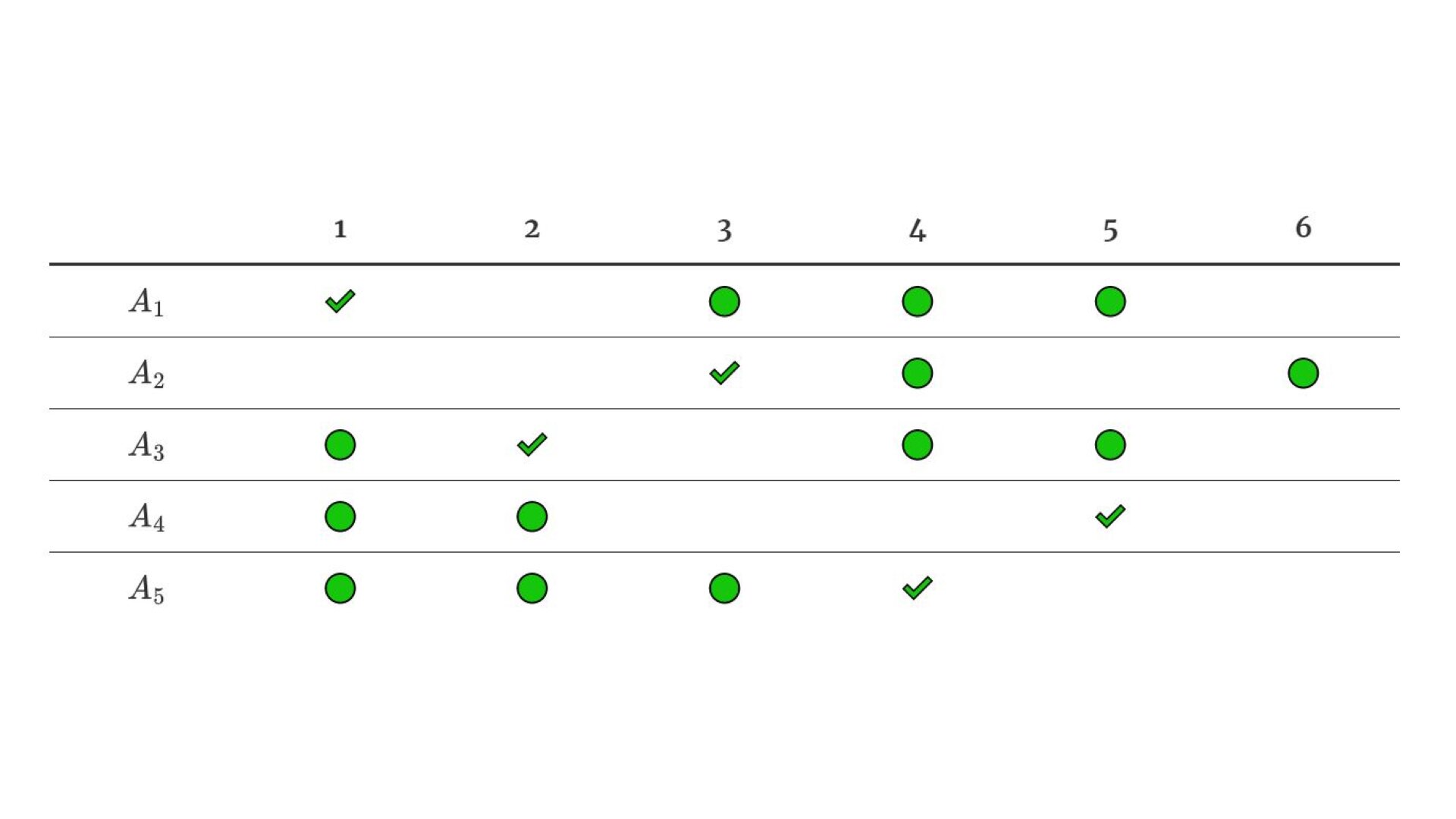
This example instance can be visualized with a table

	1	2	3	4	5	6
$A_1$	E		E	E	E
$A_2$			E	E		E
$A_3$	E	E		E	E
$A_4$	E	E			E
$A_5$	E	E	E	E

where the elements of the subsets are marked with E. In other words, we essentially want to find 5 E-cells in the above table such that no two cells that we pick have the same row or column. This instance of the problem has a solution, since we can pick, for example, the following cells marked with S:

	1	2	3	4	5	6
$A_1$	S		E	E	E
$A_2$			S	E		E
$A_3$	E	S		E	E
$A_4$	E	E			S
$A_5$	E	E	E	S

This visualization makes it also very clear why the formalization of the problem above is really equivalent to finding an injective mapping with restrictions for values — we can interpret the above table as a mapping $f : S \rightarrow \{1, 2, 3, 4, 5, 6\}$​ where $f(A_1) = 1$​, $f(A_2) = 3$​, $f(A_3) = 2$​, $f(A_4) = 5$​, $f(A_5) = 4$​. Obviously,

• if some two cells that we choose are in the same column, then $f$ is not injective,
• by definition of a mapping, no two cells can have the same row

A special case of the problem

Every injective mapping $f : A \rightarrow B$ with $\st A \st = \st B \st \in \mathbb{N}_0$ is also surjective and bijective. This leads us to an interesting special case of Restricted injective mapping, where we just add an additional constraint, that the amount of subsets in the collection $S$ must be equal to the cardinality of $A$:

Name: Restricted bijective mapping

Input: A set $A$ of cardinality $\st A \st = n$ and a collection of $n$ subsets $S = \{A_1, \dots, A_n\}$ of $A$, i.e. $A_i \subseteq A$ for all $1 \le i \le n$.

Question: $\exists (a_1, \dots, a_n) \in A_1 \times \dots \times A_n$ such that $a_i \neq a_j$ for all $i \neq j, 1 \le i,j \le n$?

In other words and in light of the above visualization of an example instance of Restricted injective mapping with a table, this special case has an additional requirement that there are exactly as many rows as columns.

Proof idea

In order to prove $\mathcal{NP}$​​​-hardness of the Restricted bijective mapping problem above, we need to construct a reduction from an already-proven $\mathcal{NP}$​​​-complete problem. This reduction must somehow express the constraints of the original problem with the collection of subsets $S$​​​. Many $\mathcal{NP}$​​​​-complete problems are graph-related and in graphs, a path with disjoint vertices seems to have very similar constraints compared to our problem. It may therefore be a good idea to let $A$ be the set of nodes $V$ in an undirected graph $G = (V, E)$ where, without loss of generality, $V = \{1, \dots, n\}$ and define $A_i$ for $1 \le i \le n$ as follows: $A_i := \{v \mid \{i, v\} \in E\}$

For example, consider the following graph with $n = 8$​ vertices:

If there exists a cycle in $G$​ that visits each node exactly once, or, in other words, a Hamiltonian circuit, like in this example where such a cycle is marked red, then, by definition of $A_i$, it holds that $\exists (a_1, \dots, a_n) \in A_1 \times \dots \times A_n : \forall 1 \le i, j \le n : i \neq j \Rightarrow a_i \neq a_j$

which means that such a reduction will lead to a yes-instance of Restricted bijective mapping. However, the converse is not true — a graph without a Hamiltonian circuit can still be reduced to a yes-instance of our problem. For example, the graph

gets reduced to $\begin{aligned} A &:= \{1, 2, 3, 4, 5, 6\} \\ S &:= \{A_1, A_2, A_3, A_4, A_5, A_6\} \\ A_1 &:= \{3, 2\} \\ A_2 &:= \{1, 3\} \\ A_3 &:= \{1, 2, 6\} \\ A_4 &:= \{5, 6\} \\ A_5 &:= \{4, 6\} \\ A_6 &:= \{3, 4, 5\} \end{aligned}$

where it is possible to choose $(a_1, a_2, a_3, a_4, a_5, a_6) = (2, 3, 1, 5, 6, 4)$

such that $a_i \neq a_j$ for $i \neq j$​​. It is clear that this problem only arises when the graph contains multiple vertex-disjoint cycles such that every node is part of exactly one such cycle.

The Hamiltonian circuit problem is a well-known $\mathcal{NP}$​-complete problem, which is formally defined as follows:

Name: HC

Input: Undirected graph $G = (V, E)$

Question: Does there exist a hamiltonian circuit, i.e. a cycle that visits every vertex exactly once?

If we prove $\mathcal{NP}$-hardness of HC with a reduction $f$ that cannot produce graphs with two or more vertex-disjoint cycles such that every node is in exactly one such cycle, and then prove $\mathcal{NP}$-hardness of Restricted bijective mapping with a reduction $g$ that assumes that the input graph cannot be partitioned in vertex-disjoint cycles as mentioned above, then the composite reduction $g \circ f$ will prove $\mathcal{NP}$-hardness of our problem. For a formal proof I will therefore need to reiterate a variant of the well-known proof of $\mathcal{NP}$​-completeness of HC emphasizing the fact that only graphs with the above mentioned constraint are being produced.

NP-completeness of HC

This problem is obviously in $\mathcal{NP}$, because we can use a sequence of vertices as a certificate that can be verified in polynomial time by making sure that:

• this sequence of vertices is a path with disjoint vertices;
• the last vertex is connected with the first one;
• every node of the graph is in the sequence;

In order to prove $\mathcal{NP}$​​​-hardness, we will construct a polynomial-time reduction from the 3-SAT problem. Let $G(i, k)$​ be a graph with the following vertices and edges:

This gadget contains exactly the following two hamiltonian paths between $s(i)$​​​​ and $e(i)$​​​​​​ (we will drop the $(i)$​​ in node names​​ if the graph $G(i, k)$​​​ containing that vertex can be inferred from the context): $(s, s', t_0, m_0, f_0, t_1, m_1, f_1, t_2, m_2, f_2, \dots, t_k, m_k, f_k, e', e) \\ (s, s', f_0, m_0, t_0, f_1, m_1, t_1, f_2, m_2, t_2, \dots, f_k, m_k, t_k, e', e)$

This is the case because after choosing $t_0$ or $f_0$ after $s'$, the rest of the hamiltonian path is uniquely determined — $(s', t_0, f_1)$, $(s', f_0, t_1)$, $(t_j, f_{j+1}, t_{j+2})$, $(f_j, t_{j+1}, f_{j+2})$, $(t_{k-1}, f_k, e')$ and $(f_{k-1}, t_k, e')$ cannot be parts of the path since then there is no way to visit

• $f_0$ or $m_0$,
• $t_0$ or $m_0$,
• $t_{j+1}$ or $m_{j+1}$,
• $f_{j+1}$ or $m_{j+1}$,
• $t_k$ or $m_k$,
• $f_k$ or $m_k$,

respectively, and then reach $e$.

Let $\varphi$ be a 3-SAT formula with $k$ clauses and, without loss of generality, $n$ variables $x_1, \dots, x_n$ such that no variable appears positively and negatively in the same clause (otherwise remove such redundant clauses). We can construct a graph $G = (V, E)$ as follows:

• For each variable $x_i$​, add the gadget $G(i, k)$ to $G$. If $i \ge 2$, connect the current gadget with the gadget for the previous variable by creating an edge $\{e(i - 1), s(i)\} \in E$.
• For each clause $1 \le y \le k$, create a node $c(y) \in V$.
• If a positive literal $x_i$ appears in clause $1 \le y \le k$, create edges $\{c(y), f_{y-1}(i)\} \in E$ and $\{t_y(i), c(y)\} \in E$.
• If a negative literal $\neg x_i$ appears in clause $1 \le y \le k$, create edges $\{c(y), t_{y-1}(i)\} \in E$ and $\{f_y(i), c(y)\} \in E$.
• Create an edge $\{e(n), s(1)\} \in E$.

Intuitively, a hamiltonian circuit in $G$ containing $(s'(i), t_0(i))$ corresponds to a variable assignment where $x_i = \top$. Analogously, $(s'(i), f_0(i))$ in the hamiltonian circuit means that it corresponds to a variable assignment with $x_i = \bot$. By construction of $G$ and because of the fact that no variable in $\varphi$ appears in a single clause both positively and negatively, node $c(y)$ can be part of a hamiltonian circuit if an only if the hamiltonian circuit “sets” at least one literal in clause $y$ to true, as described above. Moreover, if $\{c(y), f_{y-1}(i)\} \in E$ is part of the hamiltonian circuit, then $t_y(i)$ must be the next node after $c(y)$, because otherwise it is impossible to visit all nodes because of the way gadgets are connected. The same holds for the case when $\{c(y), t_{y-1}(i)\} \in E$ is part of the hamiltonian circuit — then $f_y(i)$ must be the next node after $c(y)$. It follows from the above, that there exists a hamiltonian circuit iff $\varphi$ is satisfiable.

We now need to argue why $G$ cannot be partitioned into at least two vertex-disjoint cycles. Assume this were not the case. Then there would exist a clause $y$ such that $c(y) \in V$​ is part of a cycle that doesn’t visit every $v \in V$. If this cycle contains only $c(y)$​ and nodes within a single gadget $G(i, k)$, then there exists at least one $m_j(i)$​ in that gadget, which cannot be visited by any vertex-disjoint cycle because of the above argument that a gadget has exactly two hamiltonian paths, and we therefore get a contradiction. Otherwise the cycle must pass through at least two gadgets $G(l, k)$ and $G(m, k)$​​ and must visit the “bridge” between them, i.e either $e(l)$ and $s(m)$ or $s(l)$​ and $e(m)$​​, because otherwise at least one node out of $e(l), s(m), s(l), e(m)$​​ would not be part of a vertex-disjoint cycle. But this means that there exists no path between $s(1)$ and $e(n)$ apart from $(s(1), e(n))$ meaning that those nodes are not part of a vertex-disjoint cycle. We therefore get a contradiction.

The reduction described above is obviously a polynomial-time reduction. This completes the proof of $\mathcal{NP}$-completeness of HC.

NP-completeness of finding a bijective mapping

Restricted bijective mapping is in $\mathcal{NP}$, because $(a_1, \dots, a_n)$ can be used as a certificate. It can be verified in polynomial time that $(a_1, \dots, a_n) \in A_1 \times \dots \times A_n$ and that $a_i \neq a_j$ for all $i \neq j, 1 \le i,j \le n$.

In order to prove $\mathcal{NP}$​-hardness, we will use the idea described in the proof idea section and construct the following polynomial-time reduction from the 3-SAT problem:

• Given a 3-SAT formula $\varphi$, construct a graph $G = (V, E)$ as described in the proof of $\mathcal{NP}$-completeness of HC above. We can assume without loss of generality that $V = \{1, \dots, n\}$ as it is possible to rename vertices of $G$ efficiently.
• Let $A := \{1, \dots, n\}$.
• For each $1 \le i \le n$, compute $A_i := \{v \mid \{i, v\} \in E\}$.
• Finally, construct the collection of subsets $S := \{A_1, \dots, A_n\}$.

It follows from the correctness of the reduction in the proof of $\mathcal{NP}$-completeness of HC, that $\varphi$ is satisfiable iff $G$ has a hamiltonian circuit. In order to prove the correctness of the present reduction, we therefore need to argue why $G$ has a hamiltonian circuit if and only if: $\exists (a_1, \dots, a_n) \in A_1 \times \dots \times A_n : \forall 1 \le i, j \le n : i \neq j \Rightarrow a_i \neq a_j$

($\Rightarrow$​​): Assuming there exists a hamiltonian circuit $(p_1, \dots, p_n, p_1) \in V^{n+1}$, we can choose $(a_{p_n}, a_{p_1}, \dots, a_{p_{n-1}}) = (p_1, p_2, \dots, p_n) \in A_{p_n} \times A_{p_1} \times \dots \times A_{p_{n-1}}$

$n$ distinct values from $A_1 \times \dots \times A_n$.

($\Leftarrow$​​): Let $(a_1, \dots, a_n) \in A_1 \times \dots \times A_n$​​ such that $a_i \neq a_j$​​ for $i \neq j$​​. We can define the following mapping: $\begin{aligned} \psi : V &\rightarrow V \\ x &\mapsto a_x \end{aligned}$

It follows from the fact that $a_i$​ values are pairwise distinct, that $\psi$​ is injective. Moreover, $\psi$​ is bijective as the set of vertices $V$​​ is finite. As we argued in the np-completeness of hc section, $G$ cannot be partitioned into more than one vertex-disjoint cycle. This means that: $\forall v \in V, k \in \mathbb{N}_0 : k < n \Rightarrow\psi^k(v) \neq v$

However, because $\psi$​ is bijective and each application of $\psi$ leads to a new value in $V$, it holds that: $\forall v \in V \exists k \in \mathbb{N} : 1 \le k \le n \wedge \psi^k(v) = v$

It follows from the above two statements that $\forall v \in V : \psi^n(v) = v$

and $n$ is the minimal number of times $\psi$ must be applied to reach $v$ starting in $v$​. $G$ therefore contains $\begin{aligned} \{1, \psi(1)\} &\in E \\ \{\psi(1), \psi(\psi(1))\} &\in E \\ \{\psi(\psi(1)), \psi(\psi(\psi(1)))\} &\in E \\ \vdots \\ \{\psi^{n-2}(1), \psi^{n-1}(1)\} &\in E \\ \{\psi^{n-1}(1), \underbrace{\psi^n(1)}_{1}\} &\in E \end{aligned}$

meaning that there exists a hamiltonian circuit $(1, \psi(1), \dots, \psi^{n-1}(1), 1)$

This completes the proof.

Corollaries

NP-completeness of finding an injective mapping

Restricted injective mapping is obviously in $\mathcal{NP}$​.

The $\mathcal{NP}$​-hardness of the present problem follows directly from the $\mathcal{NP}$-hardness of Restricted bijective mapping as we can construct a trivial reduction from the latter problem that just passes the instance without any changes.

Counting the amount of injective mappings is NP-hard

Consider an instance of Restricted injective mapping, concretely a set $A$ and a collection $S = \{A_1, \dots, A_n\}$ of subsets of $A$. It may be interesting not only to determine whether we can choose $(a_1, \dots, a_n) \in A_1 \times \dots \times A_n$ such that $a_i \neq a_j$ for all $i \neq j, 1 \le i,j \le n$, but also to count the amount of such possibilities and to assess the hardness of this combinational problem. With the inclusion–exclusion principle we can count the amount of possibilities of choosing $(a_1, \dots, a_n) \notin A_1 \times \dots \times A_n$ such that $a_i \neq a_j$ for all $i \neq j, 1 \le i,j \le n$​​. Let $\overline{A_i} := A \setminus A_i$. To do that, we first define: $M_{i,u} := \{(a_1, \dots, a_n) \notin A_1 \times \dots \times A_n \mid a_i = u\}$

The above amount of possibilities of choosing the wrong tuples that still satisfy the condition $a_i \neq a_j$ for $i \neq j$ is equal to: $\gamma := \Bigg\vert \Bigg(\bigcup_{u \in \overline{A_1}} M_{1, u}\Bigg) \cup \dots \cup \Bigg(\bigcup_{u \in \overline{A_n}} M_{n, u}\Bigg)\Bigg\vert$

This formula has $O(n \cdot \st A \st)$​ terms and, given the value of $\gamma$​​, we can calculate the amount of possibilities we are interested in efficiently using the following formula: $\Bigg(\prod_{i=0}^{n - 1} (\st A \st - i)\Bigg) - \gamma$

For these reasons, the calculation of $\gamma$​​​​ is the performance bottleneck of this problem. We can calculate $\gamma$ ​using $\gamma = \sum_{k=1}^{\st I \st} (-1)^{k-1}\sum_{\substack{T \subseteq I \\ \st T \st = k}} \Big\vert \bigcap_{t \in T} M_t \Big\vert$

where $I$​​​​ is the set of indices for the set $M$​​​​ that come up in the formula for $\gamma$​​​​​, but this approach would unfortunately cause exponential blowup. The key question I now want to address is whether it may still be somehow possible to calculate $\gamma$​​​ more efficiently.

The problem

Name: Restricted injective mapping count

Input: A set $A$, collection $S = \{A_1, \dots, A_n\}$ of subsets of $A$ and $k \in \mathbb{N}_0$.

Question: Is the amount of possibilities of choosing $(a_1, \dots, a_n) \in A_1 \times \dots \times A_n$ such that $a_i \neq a_j$ for all $i \neq j, 1 \le i,j \le n$​ at least $k$?

is $\mathcal{NP}$-hard, since Restricted injective mapping can be reduced to it (with a reduction that simply sets $k := 1$ and passes the instance of the problem without any changes). We can therefore conclude, that $\gamma$ cannot be computed efficiently unless $\mathcal{P} = \mathcal{NP}$​. Intuitively, the present combinational problem uses the full power of the inclusion-exclusion principle (see this post for similar reasoning).