How propositional logic minimization and gray codes are connected

in Computer Science → Research, Logic Last modified at:
How propositional logic minimization and gray codes are connected

In this post I will introduce an interesting connection between gray codes and the problem of minimizing propositional logic formulas in disjunctive normal forms (DNF’s). Both of these concepts are related to the Hamming distance between two binary sequences, which is the amount of bits that need to be flipped in one sequence in order to obtain the other one.

Boolean functions and n-dimensional cubes

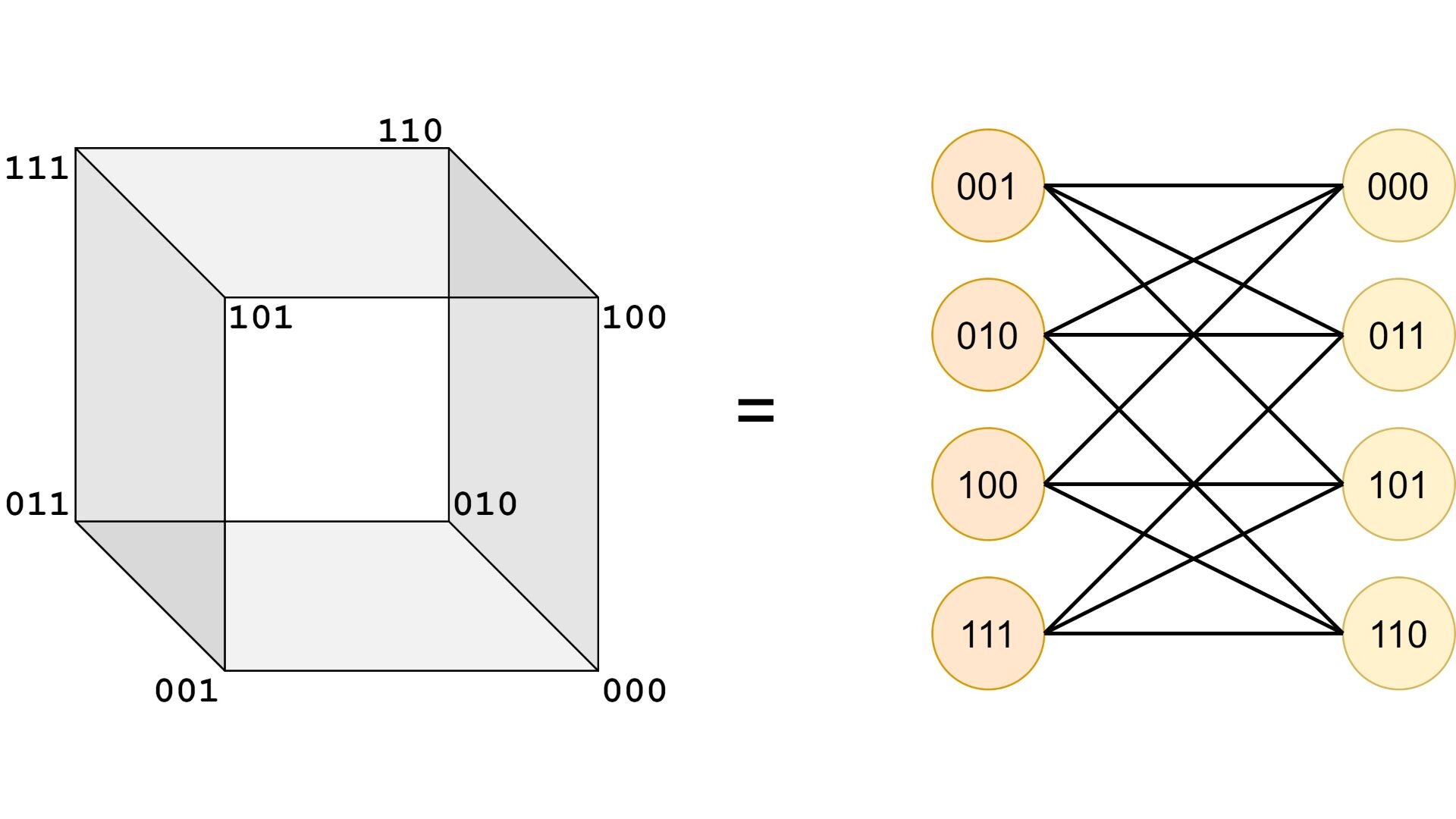
Any boolean function with nn variables can be visualized as some subset of vertices in an nn-dimensional cube. For example, for n=3n = 3, the cube looks like this:

3D boolean cube

In such cubes every edge connects vertices that correspond to variable assignments differing in exactly one variable. In other words, any disjoint n−1n - 1-dimensional sub-cubes of an nn-dimensional cube, viewed as boolean cubes (a. k. a. partial variable assignments), are adjacent.

Variable assignments that have the same number of ones can be grouped together:

3D boolean cube with nodes that have the same number of ones grouped together

It is easy to see that assignments from the blue segment have hamming distance 2 when compared with the assignments from the red segment. Analogously, this is also true for the green and brown segments. It also holds, that assignments in one segment have hamming distance 2 because of the way we grouped them. This leads us to the idea that boolean cubes are bipartite graphs if we draw edges between variable assignments that have hamming distance 1:

Boolean cubes are bipartite graphs

With the above described intuition we can now formulate and prove the following statements:

Theorem 1

Let g(x)=an−1…a0g(x) = a_{n-1}\dots a_{0} be the gray code for x:=xn−1…x0x := x_{n-1}\dots x_{0} and g(y)=bn−1…b0g(y) = b_{n-1}\dots b_{0} be the gray code for y:=yn−1…y0y := y_{n-1}\dots y_{0}. Assuming x≠yx \neq y, it holds that:

  • xx and yy are both even ⇒\Rightarrow ΔH(g(x),g(y))≥2\Delta_{\mathrm{H}}(g(x), g(y)) \ge 2.
  • xx and yy are both odd ⇒\Rightarrow ΔH(g(x),g(y))≥2\Delta_{\mathrm{H}}(g(x), g(y)) \ge 2.

Proof: by induction on BiB_i for all i∈N+i \in \mathbb{N}^{+} (I’ve defined BiB_i in this post and proved that this definition is equivalent to another definition of gray codes).

Induction base: (i=1i = 1): There is no way of choosing different xx and yy such that at least one assumption above is true, so the statements hold trivially.

Induction base: (i=2i = 2): ΔH(B2(0),B2(2))=ΔH(00,11)=2≥2ΔH(B2(1),B2(3))=ΔH(01,10)=2≥2\Delta_{\mathrm{H}}(B_2(0), B_2(2)) = \Delta_{\mathrm{H}}(00, 11) = 2 \ge 2 \\ \Delta_{\mathrm{H}}(B_2(1), B_2(3)) = \Delta_{\mathrm{H}}(01, 10) = 2 \ge 2

Induction step: (i−1→ii - 1 \rightarrow i):

  • If both Bi(x)B_i(x) and Bi(y)B_i(y) are in the first half of BiB_i, then the statements hold directly by induction hypothesis.
  • If both Bi(x)B_i(x) and Bi(y)B_i(y) are in the second half of BiB_i (formally: 2i−1≤x,y<2i2^{i-1} \le x, y < 2^i), then, by definition of BiB_i, we have:
Bi(x)=1⋅Bi−1(2i−1−1−(x−2i−1))=1⋅Bi−1(2i−1−x)Bi(y)=1⋅Bi−1(2i−1−1−(y−2i−1))=1⋅Bi−1(2i−1−y)B_i(x) = 1 \cdot B_{i-1}(2^{i-1} - 1 - (x - 2^{i-1})) = 1 \cdot B_{i-1}(2^i - 1 - x) \\ B_i(y) = 1 \cdot B_{i-1}(2^{i-1} - 1 - (y - 2^{i-1})) = 1 \cdot B_{i-1}(2^i - 1 - y)
  • So, in this case, due to x≠yx \neq y it follows that Bi−1(2i−1−x)≠Bi−1(2i−1−y)B_{i-1}(2^i - 1 - x) \neq B_{i-1}(2^i - 1 - y) and the statements hold by induction hypothesis.
  • Otherwise, without losing generality, we can assume that Bi(x)B_i(x) is in the first half of BiB_i and Bi(y)B_i(y) — in the second half of BiB_i.
  • Formally, this means 0≤x<2i−10 \le x < 2^{i-1} and 2i−1≤y<2i2^{i-1} \le y < 2^i.
  • By the definition of BiB_i, it holds that Bi(x)=0⋅Bi−1(x)B_i(x) = 0 \cdot B_{i-1}(x).
  • By the symmetry theorem I proved in this post:
Bi(y)=110…0⏟i⊕Bi−1(y−2i−1)B_i(y) = \underbrace{110 \dots 0}_{i} \oplus B_{i-1}(y - 2^{i-1})

  • If Bi−1(y−2i−1)=Bi−1(x)B_{i-1}(y - 2^{i-1}) = B_{i-1}(x), then both statements are true, because the first bit of Bi−1(y−2i−1)B_{i-1}(y - 2^{i-1}) needs to be flipped (see formula above) and the leading 1-bit of Bi(x)B_i(x) should be prepended, meaning that the hamming distance cannot be less than 2.

  • Otherwise, because subtracting 2i−12^{i-1} doesn’t affect whether yy is even or odd, we can use the induction hypothesis for xx and y−2i−1y - 2^{i-1} which states that:

ΔH(Bi−1(x),Bi−1(y−2i−1))≥2\Delta_{\mathrm{H}}(B_{i-1}(x), B_{i-1}(y - 2^{i-1})) \ge 2
  • Unfortunately, the first bit of Bi−1(y−2i−1)B_{i-1}(y - 2^{i-1}) gets flipped, so for yy, from the induction hypothesis we can only conclude that:
ΔH(0⋅Bi−1(x),010…0⏟i⊕Bi−1(y−2i−1))≥1\Delta_{\mathrm{H}}(0 \cdot B_{i-1}(x), \underbrace{010 \dots 0}_{i} \oplus B_{i-1}(y - 2^{i-1})) \ge 1

  • However, by definition of Bi(y)B_i(y) we know that a leading bit gets prepended, which increases the overall hamming distance as Bi(x)=0⋅Bi−1(x)B_i(x) = 0 \cdot B_{i-1}(x).

  • We therefore conclude that:

ΔH(0⋅Bi−1(x),010…0⏟i⊕Bi−1(y−2i−1))≥1⇒ΔH(0⋅Bi−1(x),110…0⏟i⊕Bi−1(y−2i−1))≥2⇔ΔH(Bi(x),Bi(y))≥2\begin{aligned} &\Delta_{\mathrm{H}}(0 \cdot B_{i-1}(x), \underbrace{010 \dots 0}_{i} \oplus B_{i-1}(y - 2^{i-1})) \ge 1 \\ &\Rightarrow \Delta_{\mathrm{H}}(0 \cdot B_{i-1}(x), \underbrace{110 \dots 0}_{i} \oplus B_{i-1}(y - 2^{i-1})) \ge 2 \\ &\Leftrightarrow \Delta_{\mathrm{H}}(B_i(x), B_i(y)) \ge 2 \end{aligned}

Corollary 1

nn-dimensional boolean cubes are bipartite graphs — we can partition variable assignments based on whether they are gray codes of even numbers or whether they are gray codes of odd numbers. Theorem 1 guarantees that no edges in the nn-dimensional cube connect vertices inside one group.

Hamming distance for boolean cubes

In order to prove the lemma below, we need to define hamming distance for boolean cubes. Intuitively, 2 cubes have hamming distance 1 iff there exist two assignments (vertices) in the nn-dimensional cube, such that the hamming distance between them is one, or, in other words, the shortest path between the corresponding vertices is 1.

More generally speaking, two cubes have hamming distance kk if the shortest path between some assignment of the first cube cube to some assignment from the second one is kk. For example, the hamming distance between the following boolean cubes inside an nn-dimensional cube is 2, because the shortest path (one of them is marked red) has length 2 (ΔH(001,100)=2\Delta_{\mathrm{H}}(001, 100) = 2).

Hamming distance between boolean cubes illustration

Formally, let φ:V→{0,1,∗}\varphi : V \rightarrow \{0, 1, *\} and ψ:V→{0,1,∗}\psi : V \rightarrow \{0, 1, *\} be boolean cubes. We define: ΔH(φ,ψ):=∣{v∈V:φ(v)≠∗,ψ(v)≠∗,φ(v)=1−ψ(v)}∣\Delta_{\mathrm{H}}(\varphi, \psi) := |\{v \in V : \varphi(v) \neq *, \psi(v) \neq *, \varphi(v) = 1 - \psi(v)\}|

We will first need the following statements for the proof of the main theorem (theorem 2) below:

Lemma 1

A minterm α:V→{0,1}\alpha : V \rightarrow \{0, 1\} is covered by some other implicant β:V→{0,1,∗}\beta : V \rightarrow \{0, 1, *\}, β≠α\beta \neq \alpha iff there exists some other minterm γ:V→{0,1}\gamma : V \rightarrow \{0, 1\}, γ≠α\gamma \neq \alpha, such that ΔH(α,γ)=1\Delta_{\mathrm{H}}(\alpha, \gamma) = 1.

Proof: (⇒\Rightarrow): β\beta covers α\alpha means β(x)≠∗⇒β(x)=α(x)\beta(x) \neq * \Rightarrow \beta(x) = \alpha(x) for all x∈Vx \in V. As β≠α\beta \neq \alpha, there exists at least one variable z∈Vz \in V such that β(z)=∗\beta(z) = *. We can thus define γ\gamma as follows:

  • If β(x)≠∗\beta(x) \neq *, define γ(x):=α(x)=β(x)\gamma(x) := \alpha(x) = \beta(x).
  • If β(x)=∗\beta(x) = * and x≠zx \neq z, define γ(x):=α(x)\gamma(x) := \alpha(x).
  • Finally, define γ(z):=1−α(z)\gamma(z) := 1 - \alpha(z).

By construction, it holds that ΔH(α,γ)=1\Delta_{\mathrm{H}}(\alpha, \gamma) = 1 and γ≠α\gamma \neq \alpha.

(⇐\Leftarrow): If there exists a γ≠α\gamma \neq \alpha with ΔH(α,γ)=1\Delta_{\mathrm{H}}(\alpha, \gamma) = 1, then, by definition of ΔH\Delta_{\mathrm{H}}, there exists exactly one variable z∈Vz \in V such that α(z)=1−γ(z)\alpha(z) = 1 - \gamma(z) and for all other variables x∈Vx \in V, x≠zx \neq z it holds that α(x)=γ(z)\alpha(x) = \gamma(z). We define β\beta accordingly:

  • If x≠zx \neq z, set β(x):=α(x)=γ(z)\beta(x) := \alpha(x) = \gamma(z).
  • Set β(z):=∗\beta(z) := *.

By construction, β≠α\beta \neq \alpha covers α\alpha.

Corollary 2

A minterm α:V→{0,1}\alpha : V \rightarrow \{0, 1\} is a prime implicant iff for all other minterms γ:V→{0,1}\gamma : V \rightarrow \{0, 1\}, γ≠α\gamma \neq \alpha the hamming distance ΔH(α,γ)≥2\Delta_{\mathrm{H}}(\alpha, \gamma) \ge 2.

Proof: By definition, a cube is a prime implicant iff it is not covered by any other implicant. Accordingly, a minterm α:V→{0,1}\alpha : V \rightarrow \{0, 1\} (each minterm is also a cube) is a prime implicant iff it is not covered by any other implicant. Not being covered by any other implicant means, by the lemma 1 above, that for all other minterms γ:V→{0,1}\gamma : V \rightarrow \{0, 1\}, γ≠α\gamma \neq \alpha the hamming distance ΔH(α,γ)≥2\Delta_{\mathrm{H}}(\alpha, \gamma) \ge 2.

Corollary 3

There exist at most 2n−12^{n-1} models that are prime implicants.

Proof: Corollary 2, taken in conjunction with the fact that every vertex in the nn-dimensional cube has nn adjacent vertices, implies that it is impossible to choose k>2n−1k > 2^{n-1} models (out of 2n2^n variable assignments) such that no models among them have hamming distance 1. Accordingly, there cannot exist k>2n−1k > 2^{n-1} (different) models that are prime implicants.

Corollary 4

There are at most 2n−12^{n-1} (distinct) essential prime implicants.

Proof:

  • Suppose we managed to pick k>2n−1k > 2^{n-1} essential prime implicants — let the set PP contain them — ∣P∣=k\st P \st = k.
  • Every p∈Pp \in P is essential. Intuitively, this means that it must contribute at least one model that other essential prime implicants in PP cannot contribute.
  • Formally, it holds that for every p∈Pp \in P there exists a model mpm_p, such that there is no other q∈Pq \in P, q≠pq \neq p, that contains this model (M(q)M(q) denotes the set of models qq covers):
∀p,q∈P:p≠q:mp∉M(q)\forall p, q \in P : p \neq q : m_p \notin M(q)
  • It follows that models {mp:p∈P}\{m_p : p \in P\} must have hamming distance 1 among each other.
  • This means, by corollary 2, that all these models by themselves must be prime implicants.
  • We get a contradiction, because corollary 3 states that it is impossible to choose k>2n−1k > 2^{n-1} models that are prime implicants.

Theorem 2

For any n∈N+n \in \mathbb{N}^+, there exist exactly 2 boolean functions φ\varphi and ψ\psi with nn variables, such that the smallest possible DNF’s describing these functions consist of 2n−12^{n-1} terms and each term has exactly nn literals. All other boolean functions with nn variables have smaller minimal DNF’s.

Moreover, φ\varphi and ψ\psi have the following properties: φ(xn−1,…,x0)=1⇔∃k∈N0:xn−1…x0=g(2⋅k)ψ(xn−1,…,x0)=1⇔∃k∈N0:xn−1…x0=g(2⋅k+1)φ≡¬ψφ(xn−1,…,x0)≡xn−1⊕⋯⊕x0ψ(xn−1,…,x0)≡xn−1↔⋯↔x0\begin{aligned} \varphi(x_{n-1}, \dots, x_0) = 1 &\Leftrightarrow \exists k \in \mathbb{N}_0 : x_{n-1}\dots x_0 = g(2 \cdot k) \\ \psi(x_{n-1}, \dots, x_0) = 1 &\Leftrightarrow \exists k \in \mathbb{N}_0 : x_{n-1}\dots x_0 = g(2 \cdot k + 1) \\ \varphi &\equiv \neg \psi \\ \varphi(x_{n-1}, \dots, x_0) &\equiv x_{n-1} \oplus \dots \oplus x_0 \\ \psi(x_{n-1}, \dots, x_0) &\equiv x_{n-1} \leftrightarrow \dots \leftrightarrow x_0 \end{aligned}

Proof: Each boolean function is a set of models. Clearly, this set is a subset of the set of vertices of an nn-dimensional cube, built as described at the beginning of this post.

By the theorem 1 above, stating that gray codes for even numbers have hamming distance at least 2 among each other, combined with corollary 2, it follows that all 2n−12^{n-1} models of φ\varphi are prime implicants. Analogously, all 2n−12^{n-1} models of ψ\psi are prime implicants. Corollary 3 states, that there exist at most 2n−12^{n-1} models that are prime implicants, so we conclude that φ\varphi and ψ\psi reach this maximum.

We now argue why it also follows that there are no other ways of choosing 2n−12^{n-1} models that are prime implicants, apart from the ways models for φ\varphi and ψ\psi — M(φ)M(\varphi) and M(ψ)M(\psi) are chosen:

  • Assume we found 2n−12^{n-1} models which are prime implicants. Let AA be the set of these models.
  • Also, assume A≠M(φ)A \neq M(\varphi) and A≠M(ψ)A \neq M(\psi).
  • This means that A∩M(φ)≠∅A \cap M(\varphi) \neq \varnothing and A∩M(ψ)≠∅A \cap M(\psi) \neq \varnothing, or, in other words, there exist variable models i,j∈Ai,j \in A, i≠ji \neq j, such that i∈M(φ)i \in M(\varphi) and j∈M(ψ)j \in M(\psi).
  • As i∈M(φ)i \in M(\varphi), because a vertex in an nn-dimensional cube has nn adjacent vertices, there exists Nψ⊆M(ψ)N_\psi \subseteq M(\psi) with ∣Nψ∣=n\st N_\psi \st = n and Nψ∩A=∅N_\psi \cap A = \varnothing.
  • If it is not he case, that Nψ∩A=∅N_\psi \cap A = \varnothing (for example, if j∈Nψj \in N_\psi), then we directly get a contradiction.
  • Analogously, there exists Nφ⊆M(ψ)N_\varphi \subseteq M(\psi) with ∣Nφ∣=n\st N_\varphi \st = n and Nφ∩A=∅N_\varphi \cap A = \varnothing.
  • Therefore, it holds that A⊆M\(Nφ∪Nψ)A \subseteq M \backslash (N_\varphi \cup N_\psi), where MM is the set of all models. Note that NφN_\varphi and NψN_\psi are disjoint. In other words, AA contains models from the remaining 2n−2⋅n2^n - 2 \cdot n vertices of the cube.
  • Suppose we we know all 2n−1−22^{n-1} - 2 vertices apart from ii and jj that are in AA (these nodes are “chosen” out of 2n−2⋅n−22^n - 2 \cdot n - 2 remaining vertices).
  • We now estimate the maximum number of edges that are not inside AA, i.e. that either connect nodes outside AA with each other or connect nodes inside AA with nodes outside of AA:
(2n−2⋅n−2n−1+n)⋅n=(2n−2n−1−n)⋅n=(2n−1−n)⋅n\begin{aligned} (2^n - 2 \cdot n - 2^{n-1} + n) \cdot n &= (2^n - 2^{n-1} - n) \cdot n \\ &= (2^{n-1} - n) \cdot n \end{aligned}
  • There are 2n−1⋅n2^{n-1} \cdot n edges total. So, at least the following amount of edges must connect nodes inside AA:
2n−1⋅n−(2n−1−n)⋅n=(2n−1−(2n−1−n))⋅n=(2n−1−2n−1+n)⋅n=n2\begin{aligned} 2^{n-1} \cdot n - (2^{n-1} - n) \cdot n &= (2^{n-1} - (2^{n-1} - n)) \cdot n \\ &= (2^{n-1} - 2^{n-1} + n) \cdot n \\ &= n^2 \end{aligned}
  • We therefore get a contradiction.

The above reasoning can be visualized for n=5n = 5 as follows (we consider the worst-case AA set in this visualization):

Visualization of the uniqueness of phi and psi models proof

It follows from the above that φ\varphi and ψ\psi are exactly the boolean functions which have the most models that are prime implicants — all other boolean functions have less.

Now, we will need the Quine’s Theorem, which reads as follows:

Each minimal disjunction of cubes is a disjunction of prime implicants.

In the present context, because of corollary 4 stating that there are at most 2n−12^{n-1} essential prime implicants, this means that every minimal DNF has at most 2n−12^{n-1} terms (each term satisfies the whole formula iff the variable assignment is described by the corresponding prime implicant).

All (essential) prime implicants of φ\varphi and ψ\psi are models, so each term in the minimal DNF is guaranteed to have nn literals, making it the maximal DNF possible:

  • If some other boolean function has less than 2n−12^{n-1} essential prime implicants, it will have less than 2n−12^{n-1} terms in the minimal DNF.
  • If some other boolean function has 2n−12^{n-1} essential prime implicants, then there will be at least one cube of order at least 1, making the corresponding term of the minimal DNF have less than nn literals.

The properties of the φ\varphi and ψ\psi functions mentioned in the statement of this theorem hold by construction of the models — gray codes of even numbers have an even number of ones and gray codes of odd numbers have an odd number of ones. This is not hard to prove — but it is also not necessary at this point because of the above argument about the uniqueness of the sets of models. This was also the idea I mentioned at the beginning of the post. It also follows that φ≡¬ψ\varphi \equiv \neg \psi, because both φ\varphi and ψ\psi have 2n−12^{n-1} disjoint models out of 2n2^n possible variable assignments.

This completes the proof.

Example

Consider all boolean functions with n:=3n := 3 variables. There are 2(2n)=28=2562^{(2^n)} = 2^8 = 256 such functions. These are the minimal DNF’s of all these 256 functions (I computed them with the Quine-McCluskey algorithm), the first 8 columns of the table represent the right-hand side of the truth table. The order of the assignments in the truth table is the order in which we count in binary. Please note there may be different minimal DNF’s that correspond to a particular boolean function, if that is the case then the corresponding table entry contains one of them.

R1R2R3R4R5R6R7R8Minimal DNF
000000000
00000001a ∧ b ∧ c
00000010a ∧ b ∧ ¬c
00000011a ∧ b
00000100a ∧ ¬b ∧ c
00000101a ∧ c
00000110a ∧ ¬b ∧ c ∨ a ∧ b ∧ ¬c
00000111a ∧ c ∨ a ∧ b
00001000a ∧ ¬b ∧ ¬c
00001001a ∧ ¬b ∧ ¬c ∨ a ∧ b ∧ c
00001010a ∧ ¬c
00001011a ∧ ¬c ∨ a ∧ b
00001100a ∧ ¬b
00001101a ∧ ¬b ∨ a ∧ c
00001110a ∧ ¬b ∨ a ∧ ¬c
00001111a
00010000¬a ∧ b ∧ c
00010001b ∧ c
00010010¬a ∧ b ∧ c ∨ a ∧ b ∧ ¬c
00010011b ∧ c ∨ a ∧ b
00010100¬a ∧ b ∧ c ∨ a ∧ ¬b ∧ c
00010101b ∧ c ∨ a ∧ c
00010110¬a ∧ b ∧ c ∨ a ∧ ¬b ∧ c ∨ a ∧ b ∧ ¬c
00010111b ∧ c ∨ a ∧ c ∨ a ∧ b
00011000a ∧ ¬b ∧ ¬c ∨ ¬a ∧ b ∧ c
00011001a ∧ ¬b ∧ ¬c ∨ b ∧ c
00011010¬a ∧ b ∧ c ∨ a ∧ ¬c
00011011a ∧ ¬c ∨ b ∧ c
00011100¬a ∧ b ∧ c ∨ a ∧ ¬b
00011101a ∧ ¬b ∨ b ∧ c
00011110¬a ∧ b ∧ c ∨ a ∧ ¬b ∨ a ∧ ¬c
00011111b ∧ c ∨ a
00100000¬a ∧ b ∧ ¬c
00100001¬a ∧ b ∧ ¬c ∨ a ∧ b ∧ c
00100010b ∧ ¬c
00100011b ∧ ¬c ∨ a ∧ b
00100100¬a ∧ b ∧ ¬c ∨ a ∧ ¬b ∧ c
00100101¬a ∧ b ∧ ¬c ∨ a ∧ c
00100110a ∧ ¬b ∧ c ∨ b ∧ ¬c
00100111b ∧ ¬c ∨ a ∧ c
00101000¬a ∧ b ∧ ¬c ∨ a ∧ ¬b ∧ ¬c
00101001¬a ∧ b ∧ ¬c ∨ a ∧ ¬b ∧ ¬c ∨ a ∧ b ∧ c
00101010b ∧ ¬c ∨ a ∧ ¬c
00101011b ∧ ¬c ∨ a ∧ ¬c ∨ a ∧ b
00101100¬a ∧ b ∧ ¬c ∨ a ∧ ¬b
00101101¬a ∧ b ∧ ¬c ∨ a ∧ ¬b ∨ a ∧ c
00101110b ∧ ¬c ∨ a ∧ ¬b
00101111b ∧ ¬c ∨ a
00110000¬a ∧ b
00110001¬a ∧ b ∨ b ∧ c
00110010¬a ∧ b ∨ b ∧ ¬c
00110011b
00110100a ∧ ¬b ∧ c ∨ ¬a ∧ b
00110101¬a ∧ b ∨ a ∧ c
00110110a ∧ ¬b ∧ c ∨ ¬a ∧ b ∨ b ∧ ¬c
00110111a ∧ c ∨ b
00111000a ∧ ¬b ∧ ¬c ∨ ¬a ∧ b
00111001a ∧ ¬b ∧ ¬c ∨ ¬a ∧ b ∨ b ∧ c
00111010¬a ∧ b ∨ a ∧ ¬c
00111011a ∧ ¬c ∨ b
00111100¬a ∧ b ∨ a ∧ ¬b
00111101¬a ∧ b ∨ a ∧ ¬b ∨ a ∧ c
00111110¬a ∧ b ∨ a ∧ ¬b ∨ a ∧ ¬c
00111111b ∨ a
01000000¬a ∧ ¬b ∧ c
01000001¬a ∧ ¬b ∧ c ∨ a ∧ b ∧ c
01000010¬a ∧ ¬b ∧ c ∨ a ∧ b ∧ ¬c
01000011¬a ∧ ¬b ∧ c ∨ a ∧ b
01000100¬b ∧ c
01000101¬b ∧ c ∨ a ∧ c
01000110a ∧ b ∧ ¬c ∨ ¬b ∧ c
01000111¬b ∧ c ∨ a ∧ b
01001000¬a ∧ ¬b ∧ c ∨ a ∧ ¬b ∧ ¬c
01001001¬a ∧ ¬b ∧ c ∨ a ∧ ¬b ∧ ¬c ∨ a ∧ b ∧ c
01001010¬a ∧ ¬b ∧ c ∨ a ∧ ¬c
01001011¬a ∧ ¬b ∧ c ∨ a ∧ ¬c ∨ a ∧ b
01001100¬b ∧ c ∨ a ∧ ¬b
01001101¬b ∧ c ∨ a ∧ ¬b ∨ a ∧ c
01001110¬b ∧ c ∨ a ∧ ¬c
01001111¬b ∧ c ∨ a
01010000¬a ∧ c
01010001¬a ∧ c ∨ b ∧ c
01010010a ∧ b ∧ ¬c ∨ ¬a ∧ c
01010011¬a ∧ c ∨ a ∧ b
01010100¬a ∧ c ∨ ¬b ∧ c
01010101c
01010110a ∧ b ∧ ¬c ∨ ¬a ∧ c ∨ ¬b ∧ c
01010111a ∧ b ∨ c
01011000a ∧ ¬b ∧ ¬c ∨ ¬a ∧ c
01011001a ∧ ¬b ∧ ¬c ∨ ¬a ∧ c ∨ b ∧ c
01011010¬a ∧ c ∨ a ∧ ¬c
01011011¬a ∧ c ∨ a ∧ ¬c ∨ a ∧ b
01011100¬a ∧ c ∨ a ∧ ¬b
01011101a ∧ ¬b ∨ c
01011110¬a ∧ c ∨ a ∧ ¬b ∨ a ∧ ¬c
01011111c ∨ a
01100000¬a ∧ ¬b ∧ c ∨ ¬a ∧ b ∧ ¬c
01100001¬a ∧ ¬b ∧ c ∨ ¬a ∧ b ∧ ¬c ∨ a ∧ b ∧ c
01100010¬a ∧ ¬b ∧ c ∨ b ∧ ¬c
01100011¬a ∧ ¬b ∧ c ∨ b ∧ ¬c ∨ a ∧ b
01100100¬a ∧ b ∧ ¬c ∨ ¬b ∧ c
01100101¬a ∧ b ∧ ¬c ∨ ¬b ∧ c ∨ a ∧ c
01100110¬b ∧ c ∨ b ∧ ¬c
01100111¬b ∧ c ∨ b ∧ ¬c ∨ a ∧ b
01101000¬a ∧ ¬b ∧ c ∨ ¬a ∧ b ∧ ¬c ∨ a ∧ ¬b ∧ ¬c
01101001¬a ∧ ¬b ∧ c ∨ ¬a ∧ b ∧ ¬c ∨ a ∧ ¬b ∧ ¬c ∨ a ∧ b ∧ c
01101010¬a ∧ ¬b ∧ c ∨ b ∧ ¬c ∨ a ∧ ¬c
01101011¬a ∧ ¬b ∧ c ∨ b ∧ ¬c ∨ a ∧ ¬c ∨ a ∧ b
01101100¬a ∧ b ∧ ¬c ∨ ¬b ∧ c ∨ a ∧ ¬b
01101101¬a ∧ b ∧ ¬c ∨ ¬b ∧ c ∨ a ∧ ¬b ∨ a ∧ c
01101110¬b ∧ c ∨ b ∧ ¬c ∨ a ∧ ¬c
01101111¬b ∧ c ∨ b ∧ ¬c ∨ a
01110000¬a ∧ c ∨ ¬a ∧ b
01110001¬a ∧ c ∨ ¬a ∧ b ∨ b ∧ c
01110010¬a ∧ c ∨ b ∧ ¬c
01110011¬a ∧ c ∨ b
01110100¬b ∧ c ∨ ¬a ∧ b
01110101¬a ∧ b ∨ c
01110110¬b ∧ c ∨ ¬a ∧ b ∨ b ∧ ¬c
01110111c ∨ b
01111000a ∧ ¬b ∧ ¬c ∨ ¬a ∧ c ∨ ¬a ∧ b
01111001a ∧ ¬b ∧ ¬c ∨ ¬a ∧ c ∨ ¬a ∧ b ∨ b ∧ c
01111010¬a ∧ c ∨ b ∧ ¬c ∨ a ∧ ¬c
01111011¬a ∧ c ∨ a ∧ ¬c ∨ b
01111100¬b ∧ c ∨ ¬a ∧ b ∨ a ∧ ¬b
01111101¬a ∧ b ∨ a ∧ ¬b ∨ c
01111110¬a ∧ c ∨ b ∧ ¬c ∨ a ∧ ¬b
01111111c ∨ b ∨ a
10000000¬a ∧ ¬b ∧ ¬c
10000001¬a ∧ ¬b ∧ ¬c ∨ a ∧ b ∧ c
10000010¬a ∧ ¬b ∧ ¬c ∨ a ∧ b ∧ ¬c
10000011¬a ∧ ¬b ∧ ¬c ∨ a ∧ b
10000100¬a ∧ ¬b ∧ ¬c ∨ a ∧ ¬b ∧ c
10000101¬a ∧ ¬b ∧ ¬c ∨ a ∧ c
10000110¬a ∧ ¬b ∧ ¬c ∨ a ∧ ¬b ∧ c ∨ a ∧ b ∧ ¬c
10000111¬a ∧ ¬b ∧ ¬c ∨ a ∧ c ∨ a ∧ b
10001000¬b ∧ ¬c
10001001a ∧ b ∧ c ∨ ¬b ∧ ¬c
10001010¬b ∧ ¬c ∨ a ∧ ¬c
10001011¬b ∧ ¬c ∨ a ∧ b
10001100¬b ∧ ¬c ∨ a ∧ ¬b
10001101¬b ∧ ¬c ∨ a ∧ c
10001110¬b ∧ ¬c ∨ a ∧ ¬b ∨ a ∧ ¬c
10001111¬b ∧ ¬c ∨ a
10010000¬a ∧ ¬b ∧ ¬c ∨ ¬a ∧ b ∧ c
10010001¬a ∧ ¬b ∧ ¬c ∨ b ∧ c
10010010¬a ∧ ¬b ∧ ¬c ∨ ¬a ∧ b ∧ c ∨ a ∧ b ∧ ¬c
10010011¬a ∧ ¬b ∧ ¬c ∨ b ∧ c ∨ a ∧ b
10010100¬a ∧ ¬b ∧ ¬c ∨ ¬a ∧ b ∧ c ∨ a ∧ ¬b ∧ c
10010101¬a ∧ ¬b ∧ ¬c ∨ b ∧ c ∨ a ∧ c
10010110¬a ∧ ¬b ∧ ¬c ∨ ¬a ∧ b ∧ c ∨ a ∧ ¬b ∧ c ∨ a ∧ b ∧ ¬c
10010111¬a ∧ ¬b ∧ ¬c ∨ b ∧ c ∨ a ∧ c ∨ a ∧ b
10011000¬a ∧ b ∧ c ∨ ¬b ∧ ¬c
10011001¬b ∧ ¬c ∨ b ∧ c
10011010¬a ∧ b ∧ c ∨ ¬b ∧ ¬c ∨ a ∧ ¬c
10011011¬b ∧ ¬c ∨ b ∧ c ∨ a ∧ b
10011100¬a ∧ b ∧ c ∨ ¬b ∧ ¬c ∨ a ∧ ¬b
10011101¬b ∧ ¬c ∨ b ∧ c ∨ a ∧ c
10011110¬a ∧ b ∧ c ∨ ¬b ∧ ¬c ∨ a ∧ ¬b ∨ a ∧ ¬c
10011111¬b ∧ ¬c ∨ b ∧ c ∨ a
10100000¬a ∧ ¬c
10100001a ∧ b ∧ c ∨ ¬a ∧ ¬c
10100010¬a ∧ ¬c ∨ b ∧ ¬c
10100011¬a ∧ ¬c ∨ a ∧ b
10100100a ∧ ¬b ∧ c ∨ ¬a ∧ ¬c
10100101¬a ∧ ¬c ∨ a ∧ c
10100110a ∧ ¬b ∧ c ∨ ¬a ∧ ¬c ∨ b ∧ ¬c
10100111¬a ∧ ¬c ∨ a ∧ c ∨ a ∧ b
10101000¬a ∧ ¬c ∨ ¬b ∧ ¬c
10101001a ∧ b ∧ c ∨ ¬a ∧ ¬c ∨ ¬b ∧ ¬c
10101010¬c
10101011a ∧ b ∨ ¬c
10101100¬a ∧ ¬c ∨ a ∧ ¬b
10101101¬a ∧ ¬c ∨ a ∧ ¬b ∨ a ∧ c
10101110a ∧ ¬b ∨ ¬c
10101111¬c ∨ a
10110000¬a ∧ ¬c ∨ ¬a ∧ b
10110001¬a ∧ ¬c ∨ b ∧ c
10110010¬a ∧ ¬c ∨ ¬a ∧ b ∨ b ∧ ¬c
10110011¬a ∧ ¬c ∨ b
10110100a ∧ ¬b ∧ c ∨ ¬a ∧ ¬c ∨ ¬a ∧ b
10110101¬a ∧ ¬c ∨ b ∧ c ∨ a ∧ c
10110110a ∧ ¬b ∧ c ∨ ¬a ∧ ¬c ∨ ¬a ∧ b ∨ b ∧ ¬c
10110111¬a ∧ ¬c ∨ a ∧ c ∨ b
10111000¬b ∧ ¬c ∨ ¬a ∧ b
10111001¬b ∧ ¬c ∨ ¬a ∧ b ∨ b ∧ c
10111010¬a ∧ b ∨ ¬c
10111011¬c ∨ b
10111100¬b ∧ ¬c ∨ ¬a ∧ b ∨ a ∧ ¬b
10111101¬a ∧ ¬c ∨ a ∧ ¬b ∨ b ∧ c
10111110¬a ∧ b ∨ a ∧ ¬b ∨ ¬c
10111111¬c ∨ b ∨ a
11000000¬a ∧ ¬b
11000001a ∧ b ∧ c ∨ ¬a ∧ ¬b
11000010a ∧ b ∧ ¬c ∨ ¬a ∧ ¬b
11000011¬a ∧ ¬b ∨ a ∧ b
11000100¬a ∧ ¬b ∨ ¬b ∧ c
11000101¬a ∧ ¬b ∨ a ∧ c
11000110a ∧ b ∧ ¬c ∨ ¬a ∧ ¬b ∨ ¬b ∧ c
11000111¬a ∧ ¬b ∨ a ∧ c ∨ a ∧ b
11001000¬a ∧ ¬b ∨ ¬b ∧ ¬c
11001001a ∧ b ∧ c ∨ ¬a ∧ ¬b ∨ ¬b ∧ ¬c
11001010¬a ∧ ¬b ∨ a ∧ ¬c
11001011¬a ∧ ¬b ∨ a ∧ ¬c ∨ a ∧ b
11001100¬b
11001101a ∧ c ∨ ¬b
11001110a ∧ ¬c ∨ ¬b
11001111¬b ∨ a
11010000¬a ∧ ¬b ∨ ¬a ∧ c
11010001¬a ∧ ¬b ∨ b ∧ c
11010010a ∧ b ∧ ¬c ∨ ¬a ∧ ¬b ∨ ¬a ∧ c
11010011¬a ∧ ¬b ∨ b ∧ c ∨ a ∧ b
11010100¬a ∧ ¬b ∨ ¬a ∧ c ∨ ¬b ∧ c
11010101¬a ∧ ¬b ∨ c
11010110a ∧ b ∧ ¬c ∨ ¬a ∧ ¬b ∨ ¬a ∧ c ∨ ¬b ∧ c
11010111¬a ∧ ¬b ∨ a ∧ b ∨ c
11011000¬b ∧ ¬c ∨ ¬a ∧ c
11011001¬b ∧ ¬c ∨ ¬a ∧ c ∨ b ∧ c
11011010¬b ∧ ¬c ∨ ¬a ∧ c ∨ a ∧ ¬c
11011011¬a ∧ ¬b ∨ a ∧ ¬c ∨ b ∧ c
11011100¬a ∧ c ∨ ¬b
11011101¬b ∨ c
11011110¬a ∧ c ∨ a ∧ ¬c ∨ ¬b
11011111¬b ∨ c ∨ a
11100000¬a ∧ ¬b ∨ ¬a ∧ ¬c
11100001a ∧ b ∧ c ∨ ¬a ∧ ¬b ∨ ¬a ∧ ¬c
11100010¬a ∧ ¬b ∨ b ∧ ¬c
11100011¬a ∧ ¬b ∨ b ∧ ¬c ∨ a ∧ b
11100100¬a ∧ ¬c ∨ ¬b ∧ c
11100101¬a ∧ ¬c ∨ ¬b ∧ c ∨ a ∧ c
11100110¬a ∧ ¬c ∨ ¬b ∧ c ∨ b ∧ ¬c
11100111¬a ∧ ¬b ∨ b ∧ ¬c ∨ a ∧ c
11101000¬a ∧ ¬b ∨ ¬a ∧ ¬c ∨ ¬b ∧ ¬c
11101001a ∧ b ∧ c ∨ ¬a ∧ ¬b ∨ ¬a ∧ ¬c ∨ ¬b ∧ ¬c
11101010¬a ∧ ¬b ∨ ¬c
11101011¬a ∧ ¬b ∨ a ∧ b ∨ ¬c
11101100¬a ∧ ¬c ∨ ¬b
11101101¬a ∧ ¬c ∨ a ∧ c ∨ ¬b
11101110¬b ∨ ¬c
11101111¬b ∨ ¬c ∨ a
11110000¬a
11110001b ∧ c ∨ ¬a
11110010b ∧ ¬c ∨ ¬a
11110011¬a ∨ b
11110100¬b ∧ c ∨ ¬a
11110101¬a ∨ c
11110110¬b ∧ c ∨ b ∧ ¬c ∨ ¬a
11110111¬a ∨ c ∨ b
11111000¬b ∧ ¬c ∨ ¬a
11111001¬b ∧ ¬c ∨ b ∧ c ∨ ¬a
11111010¬a ∨ ¬c
11111011¬a ∨ ¬c ∨ b
11111100¬a ∨ ¬b
11111101¬a ∨ ¬b ∨ c
11111110¬a ∨ ¬b ∨ ¬c
111111111

We see that the there exist exactly two longest minimal DNF’s that correspond to the functions that we described in theorem 2 above: φ=(¬a∧¬b∧¬c)∨(¬a∧b∧c)∨(a∧¬b∧c)∨(a∧b∧¬c)≡a⊕b⊕cψ=(¬a∧¬b∧c)∨(¬a∧b∧¬c)∨(a∧¬b∧¬c)∨(a∧b∧c)≡a↔b↔cφ≡¬ψ\begin{aligned} \varphi &= (\neg a \wedge \neg b \wedge \neg c) \vee (\neg a \wedge b \wedge c) \vee (a \wedge \neg b \wedge c) \vee (a \wedge b \wedge \neg c) \equiv a \oplus b \oplus c \\ \psi &= (\neg a \wedge \neg b \wedge c) \vee (\neg a \wedge b \wedge \neg c) \vee (a \wedge \neg b \wedge \neg c) \vee (a \wedge b \wedge c) \equiv a \leftrightarrow b \leftrightarrow c \\ \varphi &\equiv \neg \psi \end{aligned}

Copyright © 2019 — 2023 Alexander Mayorov. All rights reserved.