Gray codes and their beautiful symmetries

28.12.2020 in Computer Science → Research Last modified at: 30.12.2020

This post is about gray codes a.k.a. gray encoding of binary numbers. We will also cover some interesting properties, ideas and symmetries behind this encoding.

Gray codes

The Gray encoding is a special binary encoding for numbers, which is especially efficient for counting, because the hamming distance between any 2 successive values differ in exactly 1 bit (i.e. have Hamming distance 1). For this reason, counters in low power embedded environments are often implemented with this encoding. For example, for numbers from $0$ to $15$ the corresponding gray codes are:

Number	Gray	Number	Gray
0000	0000	1000	1100
0001	0001	1001	1101
0010	0011	1010	1111
0011	0010	1011	1110
0100	0110	1100	1010
0101	0111	1101	1011
0110	0101	1110	1001
0111	0100	1111	1000

The idea behind the increment operation is the following:

• Go through the bits of the previous gray code one-by-one starting from the rightmost bit.
• If flipping the current bit leads to a new code word, flip it and return the code word.
• Otherwise, proceed with the next bit.

Encoding

The gray code of a binary number $x = x_{n-1}, \dots, x_0$ is $g = g_{n-1}, \dots, g_0$ (right hand sides in these equations mean bit sequences), where: $g_i := \begin{cases} x_i & i = n - 1 \\ x_i \oplus x_{i+1} & i < n-1 \end{cases}$

For example, for $x = {11010}_2$, the gray code would be $g = {10111}_2$: $\begin{array}{r} \oplus \begin{array}{r} 11010\\ 01101\\ \end{array} \\ \hline \begin{array}{r} 10111 \end{array} \end{array}$

This encoding can be easily implemented, for example in Python:

def gray_encode(x: int) -> int:
    return x ^ (x >> 1)

Decoding

We can calculate the bits of $x$ by knowing the gray code $g = g_{n-1}, \dots, g_0$ as follows: $x_k = \bigoplus^{n-1}_{i=k}{g_i}$

Continuing the example above, we can decode $g = {10111}_2$ and get the initial codeword $x = {11010}_2$ by calculating the prefix sums of $g$ in this notation: $\begin{array}{r} \oplus \begin{array}{r} 10111 \\ 01011 \\ 00101 \\ 00010 \\ 00001 \\ \end{array} \\ \hline \begin{array}{r} 11010 \end{array} \end{array}$

Proof of correctness: We can prove that the formula above for decoding gray codes is correct by induction on the length $n$ of the codeword:

Induction base: $k = n - 1$: $\bigoplus^{n-1}_{i=n-1}{g_i} = g_{n-1} = x_{n-1}$

Induction step: $k > 0, k \rightarrow k - 1$: $\bigoplus^{n-1}_{i=k-1}{g_i} = g_{k-1} \oplus \bigoplus^{n-1}_{i=k}{g_i} \stackrel{\mathrm{IH}}{=} g_{k-1} \oplus x_k = x_{k-1} \oplus x_k \oplus x_k = x_{k-1}$

The implementation of the decoding algorithm is also not hard:

def gray_decode(g: int) -> int:
    b = 0
    while g != 0:
        b ^= g
        g >>= 1
    return b

Recursive definition for gray codes

We can formalize the intuition behind the increment operation above by an alternative, recursive definition for gray codes:

Let $B_i$ for $i \ge 1$ be a mapping that maps numbers from $0$ to $2^i - 1$ to the corresponding gray code as a bit string.

The first 2 gray codes are $0$ and $1$, so we define: $\begin{aligned} B_1 : \{0, 1\} &\rightarrow \{0, 1\}^* \\ 0 &\mapsto 0 \\ 1 &\mapsto 1 \end{aligned}$

For $i \ge 2$, define recursively: $\begin{aligned} B_i : \{0, \dots, 2^i - 1\} &\rightarrow \{0, 1\}^* \\ 0 &\mapsto 0 \cdot B_{i-1}(0) \\ &\quad \vdots \\ 2^{i-1} - 1 &\mapsto 0 \cdot B_{i-1}(2^{i-1} - 1) \\ 2^{i-1} &\mapsto 1 \cdot B_{i-1}(2^{i-1} - 1) \\ &\quad \vdots \\ 2^i - 1 &\mapsto 1 \cdot B_{i-1}(0) \end{aligned}$

The idea behind this definition is that we “flip” the $B_i$ mapping and prepend 1 to all of the gray codes in $B_i$ in reverse order (because of the “flip”). This is how we obtain the second half of the $B_{i+1}$ mapping. Because of the reverse order, the hamming distance between 2 successive values is always 1. We can visualize this idea of the recursive mapping for the first $2^5 = 32$ gray codes:

So, the key patterns that we see in the gray code table are the following:

• The second half of any $B_i$ is the first part of $B_i$ in reverse order with a leading 1-bit.
• In order to reverse the first part of $B_i$, it is sufficient to just flip the first bit of every gray code.

We can formalize the second very important fact with the following theorem:

Symmetry theorem

For all $i \ge 2$ and $2^{i-1} \le j < 2^i$ in the second half of $B_i$, it holds that: $\begin{aligned} B_i(j) &= 1, b_{n-1} \oplus 1, b_{n-2}, \dots, b_0 \\ b_{n-1},b_{n-2}, \dots, b_0 &:= B_{i-1}(j - 2^{i-1}) \end{aligned}$

In other words, it means that $B_i(j)$ is equal to $1 \cdot B_{i-1}(j - 2^{i-1})$ with the first bit of $B_{i-1}(j - 2^{i-1})$ flipped.

Proof: by induction on $i$:

Induction base: ($i = 2$): $\begin{aligned} B_2(2) &= 1 \cdot (B_2(0) \oplus 1) = 1 \cdot (0 \oplus 1) = 1 \cdot 1 = 11 = 1 \cdot B_1(1) \\ B_2(3) &= 1 \cdot (B_2(1) \oplus 1) = 1 \cdot (1 \oplus 1) = 1 \cdot 0 = 10 = 1 \cdot B_1(0) \end{aligned}$

Induction step: ($i - 1 \rightarrow i$):

• When defining $B_{i-1}$, we prepended bit 1 to every code $j$ in the second half ($2^{i-2} \le j < 2^{i-1}$). Because of that, it is correct to flip the first bit of $B_{i-1}(j - 2^{i-1})$.
• We now argue why it is correct to just leave other bits as-is. Consider all the bits at an arbitrary, but fixed position $0 \le k \le i - 4$ in the gray codes generated by $B_{i-1}$. Formally, let $a(l) := b_k$ where $b_{n-1}\dots b_0 := B_{i-1}(l)$ and $a := a(0), \dots, a(2^{i-2}-1), a(2^{i-2}), \dots, a(2^{i-1}-1)$.
• By definition of $B_{i-1}$, the second part of $a$ is the reversed first half of $a$, or, formally, $a(2^{i-2}), \dots, a(2^{i-1}-1) = a(2^{i-2}-1), \dots, a(0)$.
• By induction hypothesis, we know that $a(0), \dots, a(2^{i-2}-1) = a(2^{i-2}), \dots, a(2^{i-1}-1)$.
• By combining the last 2 observations, it follows that both $a(0), \dots, a(2^{i-2}-1)$ and $a(2^{i-2}), \dots, a(2^{i-1}-1)$ are palindromes.
• $a$ is a concatenation of 2 equal palindromes and is therefore also a palindrome.

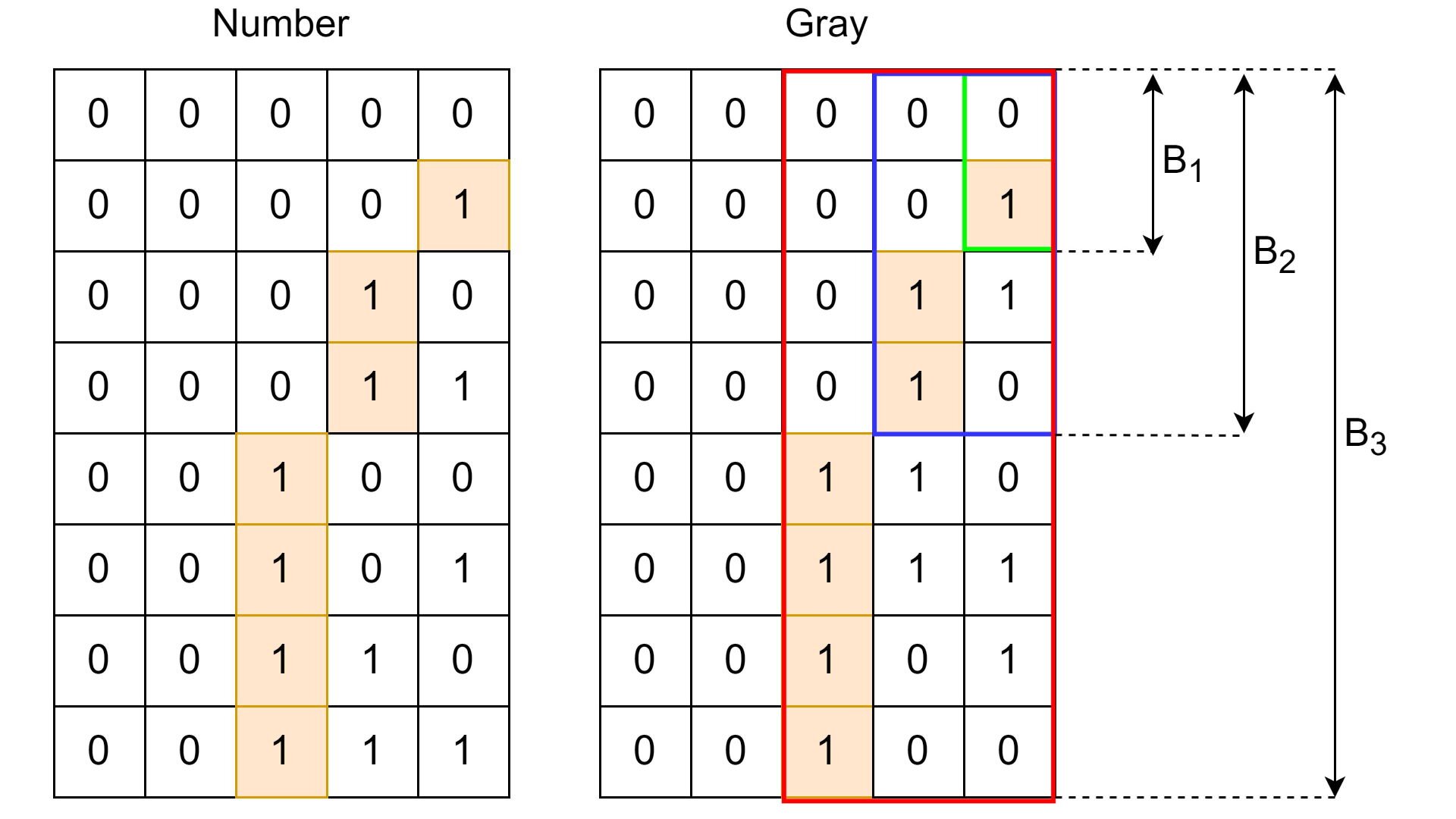
This completes the proof. We can also illustrate, for example, the $3 \rightarrow 4$ induction step:

Here, $a$ is illustrated for $k = 0$.

Equivalence of definitions

Of course, we need to prove that both definitions (recursive and non-recursive) are equivalent. Formally, we will prove the equivalence of definitions of all gray codes $0 \le x < 2^i$ by induction for all $i$:

Induction base: ($i \in \{1, 2\}$) Both definitions are equivalent for the first 4 gray codes.

Induction step: ($i \rightarrow i + 1$):

• $B_i$ is part of $B_{i+1}$, so we only need to prove that the definitions for gray codes for $2^i \le x \le 2^{i+1} - 1$ from the second part of $B_{i+1}$ are equivalent.
• Let $x = x_i, \dots, x_0$. As $B_{i+1}$ defines first $2^{i+1}$ gray codes, it follows that $x_i = 1$ (this fact is clearly seen on the illustrations above — the leading ones are marked with orange).
• By the symmetry theorem, we know that the gray code of $x$ is equal to the gray code of $x - 2^i$ with the first bit flipped and 1 prepended. On the other hand, by the first definition of gray codes and because of $B_{i+1}$ defining $2^{i+1}$ gray codes, the gray code for $x$ is also equal to the gray code of $x - 2^i$ with the first bit flipped because $g_{i-1} = x_{i-1} \oplus x_i = x_{i-1} \oplus 1$ and 1 prepended (see above). By induction hypothesis, both definitions for $x - 2^i$ were equivalent, so the definitions are equivalent for $x$.