Computing the lowest common ancestor in a full binary tree

23.09.2020 in Computer Science Last modified at: 22.10.2020

The lowest common ancestor (LCA) problem is important in many applications of binary trees. For example, by knowing the lowest common ancestor we can easily compute the shortest path between any two vertices in a tree. The most common way to compute the lca of vertices $u$ and $v$ is to iteratively go up until we get to the root of the subtree containing both $u$ and $v$. This method works only if $u$ and $v$ are on the same level. If not, we can first measure the difference of heights $d$ between $u$ and $v$ and then find the lowest common ancestor of the $d$-th parent of the lowest vertex and the higher vertex.

LCA in a full binary tree

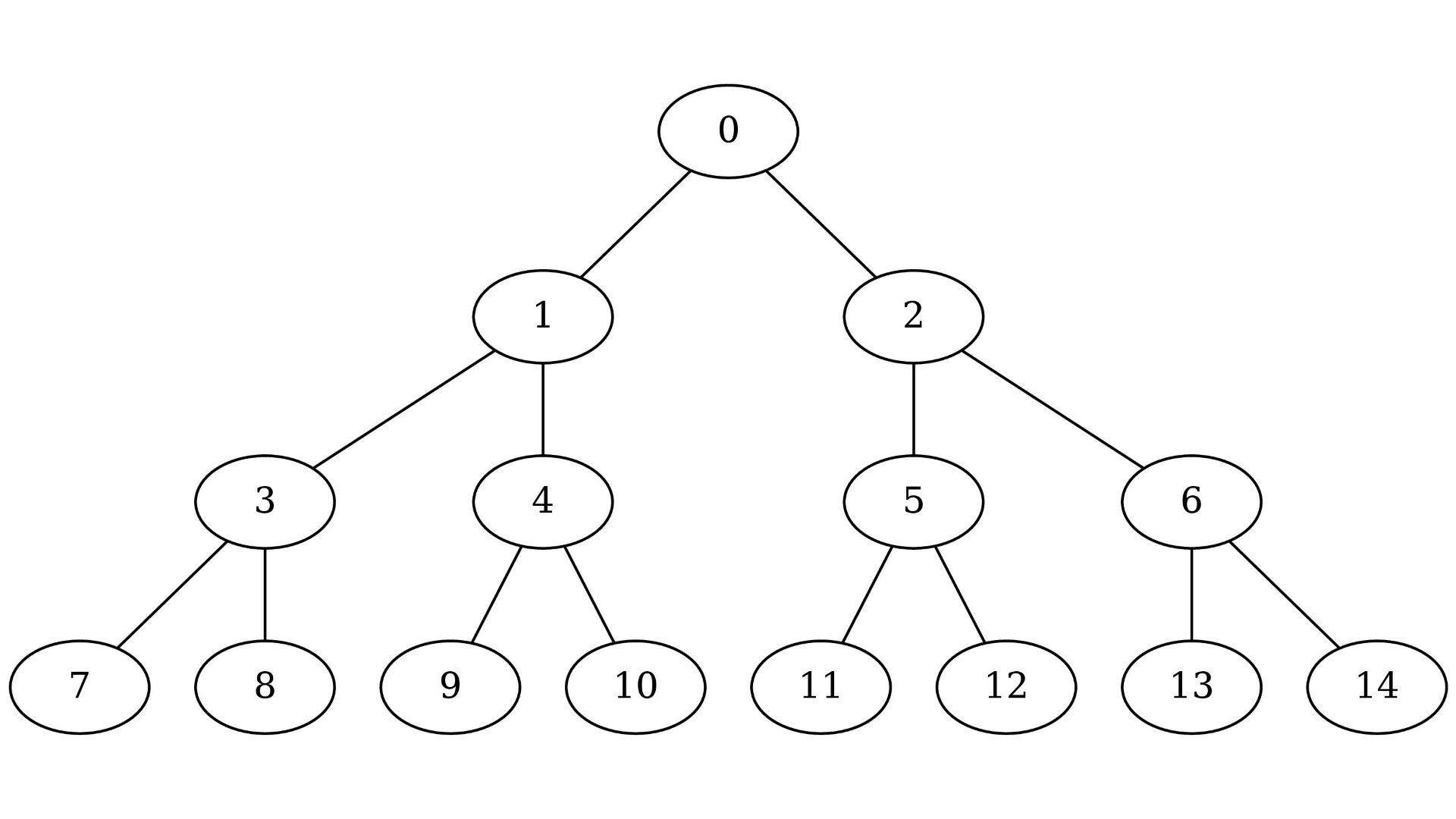
Full binary trees are often represented implicitly in memory. That means, parent-child relations are determined by looking at the positions of nodes in the array. For example, in this tree the nodes are numbered the way they will be positioned in the array:

In a full binary tree the parent of node $x$ is $p(x):=\left\lfloor\frac{x-1}{2}\right\rfloor$, and children are $2 \cdot x + 1$ and $2 \cdot x + 2$. Formally speaking, for nodes $a$ and $b$ on the same level we would like to find the value of $p^n(a)$ such that $p^n(a) = p^n(b)$ for n minimal. In binary representation, dividing by 2 and discarding the remainder is equivalent to shifting the number by 1 bit to the right. In order to use this we can just add 1 to each node index:

With this change we can implement the lca algorithm:

uint32_t lca_sameLevel(uint32_t a, uint32_t b) {
    while (a != b) {
        a >>= 1u;
        b >>= 1u;
    }
    return a;
}

This algorithm works because the lowest common ancestor is the longest common prefix of the binary representation of both nodes.

If we address nodes starting with one, then any nodewith level $l$ will be greater than or equal to $2^l$. Therefore, the amount of leading zeroes in the binary representation of nodes in the same level is equal. Moreover, the difference of amounts of leading zeroes is equal to the difference of levels. With this idea we can now implement the algorithm that correctly finds the lowest common ancestor for any pair of nodes.

uint32_t lca(uint32_t a, uint32_t b) {
    
    uint32_t aLeadingZeroes = __builtin_clz(a);
    uint32_t bLeadingZeroes = __builtin_clz(b);
    
    while (aLeadingZeroes > bLeadingZeroes) {
        b >>= 1u;
        bLeadingZeroes++;
    }
    
    while (bLeadingZeroes > aLeadingZeroes) {
        a >>= 1u;
        aLeadingZeroes++;
    }
    
    while (a != b) {
        a >>= 1u;
        b >>= 1u;
    }
    
    return a;
}

It is also easy to modify the algorithm slightly so that it works for elements indexed starting from zero.

#include <stdint.h>

uint32_t lca(uint32_t a, uint32_t b) {
    a++;
    b++;
    
    uint32_t aLeadingZeroes = __builtin_clz(a);
    uint32_t bLeadingZeroes = __builtin_clz(b);
    
    while (aLeadingZeroes > bLeadingZeroes) {
        b >>= 1u;
        bLeadingZeroes++;
    }
    
    while (bLeadingZeroes > aLeadingZeroes) {
        a >>= 1u;
        aLeadingZeroes++;
    }
    
    while (a != b) {
        a >>= 1u;
        b >>= 1u;
    }
    
    return a - 1u;
}

Complexity: $O(\log(n))$ where $n$ is the amount if nodes in the tree.

Example

If the we want to find the lowest common ancestor of 8 and 10 (indexed from zero), then we add 1 to both of them and find the longest common prefix. In this case it is the longest common prefix of 1001 and 1011 which is 10 = 2 in decimal. 2 is the lowest common ancestor in the tree with increased indices, so in the original tree the lowest common ancestor is 2 - 1 = 1.