Implementing the extended Euclidean algorithm without stack or recursion

21.02.2020 in Mathematics → Algebra Last modified at: 07.12.2020

Typical implementation of the extended Euclidean algorithm on the internet will just iteratively calculate modulo until 0 is reached. However, sometimes you also need to calculate the linear combination coefficients for the greatest common divisor.

Extended Euclidean algorithm

The extended Euclidean algorithm allows us to not only calculate the greatest common divisor of two numbers, but gives us also a representation of the result in a form of a linear combination: $\gcd(a, b) = u \cdot a + v \cdot b \quad u,v \in \mathbb{Z}$

gcd of more than 2 numbers can always be done by iteratively calculating the gcd of 2 numbers.

For example, let’s calculate $\gcd(14, 5)$: $\begin{aligned} 14 &= 5 \cdot 2 + 4 \\ 5 &= 4 \cdot 1 + 1 \\ 4 &= 1 \cdot 4 + 0 \end{aligned}$

So the greatest common divisor of $14$ and $5$ is $1$.

We can find the linear combination coefficients by writing $1$ in terms of $14$ and $5$: $\begin{aligned} 1 &= 5 - 4 \cdot 1 \\ &= 5 - (14 - 5 \cdot 2) \cdot 1 \\ &= 5 - 14 + 5 \cdot 2 \\ &= 3 \cdot 5 + (-1) \cdot 14 \end{aligned}$

So in this case $u = 3$ and $v = -1$: $\gcd(14, 5) = (-1) \cdot 14 + 3 \cdot 5 = 1$

We can calculate the linear combination coefficients by doing back substitution. But it is not so easy to implement this without recursion, because the back substitution is done when we are climbing out of the recursive calls. We will implement the algorithm recursively first.

Recursive implementation

The formula $\gcd(a, b) = \begin{cases} b, & \text{if}\ a = 0 \\ \gcd(b \bmod a, a), & \text{otherwise} \end{cases}$

allows us to describe the algorithm in a functional way:

• If $a = 0$, then the greatest common divisor is $b$. Coefficients $u = 0$ and $v = 0$.
• Else, we make the problem simpler by calculating $\gcd(b \bmod a, a)$. We can calculate the new coefficients based on the coefficients of the simpler problem.

So, how can we calculate $u$ and $v$ so that $\gcd(a, b) = u \cdot a + v \cdot b$

by knowing $u'$ and $v'$ with: $\gcd(b \bmod a, a) = u' \cdot (b \bmod a) + v' \cdot a$

In order to do that we can write $b \bmod a$ in terms of initial $a$ and $b$: $\begin{aligned} \gcd(b \bmod a, a) &= u' \cdot (b \bmod a) + v' \cdot a \\ &= u' \cdot (b - \left\lfloor \frac{b}{a} \right\rfloor \cdot a) + v' \cdot a \\ &= u' \cdot b - u' \cdot \left\lfloor \frac{b}{a} \right\rfloor \cdot a + v' \cdot a \\ &= (v' - u' \cdot \left\lfloor \frac{b}{a} \right\rfloor) \cdot a + u' \cdot b \end{aligned}$

So the new linear combination coefficients are: $\begin{aligned} u &= v' - u' \cdot \left\lfloor \frac{b}{a} \right\rfloor \\ v &= u' \end{aligned}$

With this formula we are now ready to implement the algorithm:

def extended_gcd(a: int, b: int) -> (int, int, int):
    if a == 0:
        return b, 0, 1
    (g, u, v) = extended_gcd(b % a, a)
    new_u = v - (b // a) * u
    new_v = u
    return g, new_u, new_v

Non-recursive implementation

The recursion in the algorithm above cannot be easily eliminated because the function is not tail-recursive.

In order to implement the algorithm with a loop we need to define a sequence of division remainders and then update the coefficients as we calculate the remainders. Formally, we can define a finite sequence $r_n$: $\begin{aligned} r_1 &= a \\ r_2 &= b \\ r_{n+2} &= r_n \bmod r_{n+1} \end{aligned}$

If $r_{n+1} = 0$, $r_{n+2}$ is not defined. We can write each $r_n$ as a linear combination of $u$ and $v$. Now we are interested in how $u$ and $v$ change as we calculate remainders. To do this formally, we will need to define two new finite sequences $u_n$ and $v_n$ which will represent the linear combination coefficients: $r_n = u_n \cdot a + v_n \cdot b$

By definition, $r_1 = a$ and $r_2 = b$, so we can directly write the linear combination coefficients for $r_1$ and $r_2$: $\begin{aligned} u_1 &= 1 \\ v_1 &= 0 \\ u_2 &= 0 \\ v_2 &= 1 \end{aligned}$

Let $q_n$ be the finite sequence of integer divisions in $r_n$: $r_n = r_{n+1} \cdot q_{n+2} + r_{n+2}$

Now we can write $u_n$ and $v_n$ in terms of $q_n$: $\begin{aligned} r_{n+2} &= r_n - r_{n+1} \cdot q_{n+2} \\ &= u_n \cdot a + v_n \cdot b - r_{n+1} \cdot q_{n+2} \\ &= u_n \cdot a + v_n \cdot b - (u_{n+1} \cdot a + v_{n+1} \cdot b) \cdot q_{n+2} \\ &= u_n \cdot a + v_n \cdot b - u_{n+1} \cdot a \cdot q_{n+2} - v_{n+1} \cdot b \cdot q_{n+2} \\ &= (u_n - u_{n+1} \cdot q_{n+2}) \cdot a + (v_n - v_{n+1} \cdot q_{n+2}) \cdot b \end{aligned}$

To get the formula for $u_n$ and $v_n$ we can just substitute $n$ instead of $n + 2$: $\begin{aligned} u_n &= u_{n-2} - q_n \cdot u_{n-1} \\ v_n &= v_{n-2} - q_n \cdot v_{n-1} \end{aligned}$

With this formula and the initial values of the $u_n$ and $v_n$ sequences we can now implement the extended Euclidean algorithm without recursion:

def extended_gcd(a: int, b: int) -> (int, int, int):
    if a == 0:
        # The algorithm will work correctly without this check
        # But it will take one iteration of the inner loop
        return b, 0, 1

    un_prev = 1
    vn_prev = 0
    un_cur = 0
    vn_cur = 1

    while b != 0:
        # Calculate new element of the qn sequence
        qn = a // b

        # Calculate new element of the rn sequence
        new_r = a % b
        a = b
        b = new_r

        # Calculate new coefficients with the formula above
        un_new = un_prev - qn * un_cur
        vn_new = vn_prev - qn * vn_cur

        # Shift coefficients
        un_prev = un_cur
        vn_prev = vn_cur
        un_cur = un_new
        vn_cur = vn_new

    return a, un_prev, vn_prev

Example

We can visualize the finite sequences we defined and see how the algorithm works with a table. We will calculate $\gcd(104, 47)$ and it’s linear combination coefficients: $\gcd(104, 47) = u \cdot 104 + v \cdot 47$

$r_n$	$q_n$	$u_n$	$v_n$
104	-	1	0
47	-	0	1
10	2	1	-2
7	4	-4	9
3	1	5	-11
1	2	-14	31
0	3	33	20

At each step we first calculate the next element from the $q_n$ sequence and then use it to calculate new linear combination coefficients $u_n$ and $v_n$.

The result of the algorithm: $\gcd(104, 47) = -14 \cdot 104 + 31 \cdot 47 = 1$

Improvement of the non-recusive solution

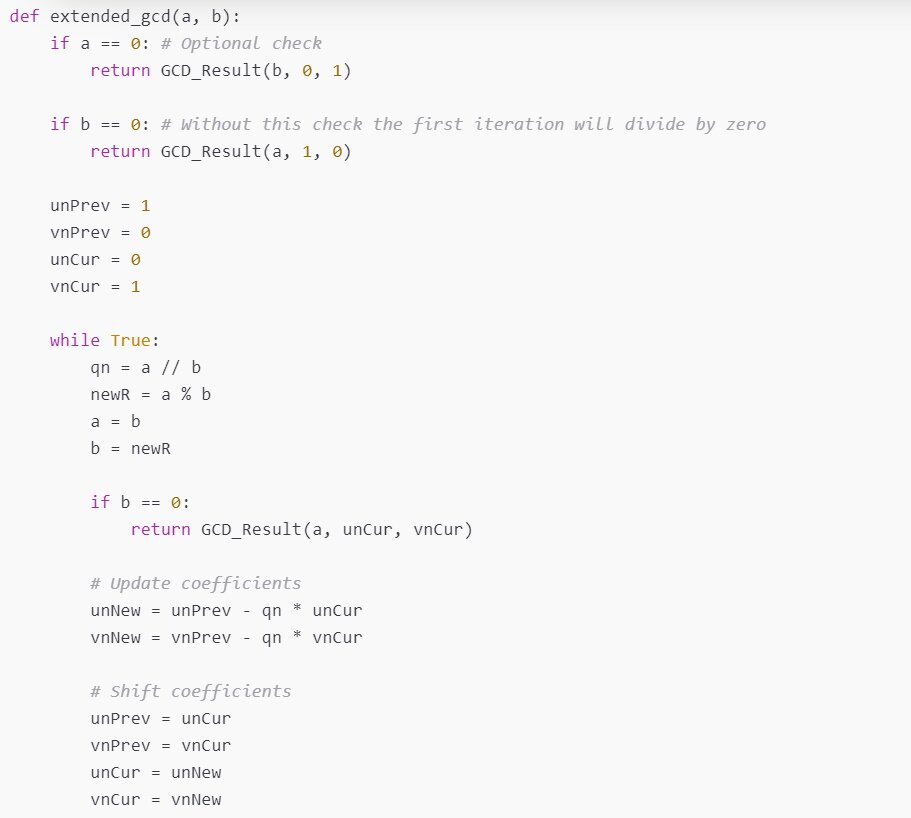
As we see in the example above, we don’t need to calculate the last row of the table because we aren’t interested in the linear combination that forms zero. We can terminate the algorithm directly after calculating the new element of the $r_n$ sequence:

def extended_gcd(a: int, b: int) -> (int, int, int):
    if a == 0: # Optional check
        return b, 0, 1

    if b == 0: # Without this check the first iteration will divide by zero
        return a, 1, 0

    un_prev = 1
    vn_prev = 0
    un_cur = 0
    vn_cur = 1

    while True:
        qn = a // b
        new_r = a % b
        a = b
        b = new_r

        if b == 0:
            return a, un_cur, vn_cur

        # Update coefficients
        un_new = un_prev - qn * un_cur
        vn_new = vn_prev - qn * vn_cur

        # Shift coefficients
        un_prev = un_cur
        vn_prev = vn_cur
        un_cur = un_new
        vn_cur = vn_new